В 2020 году планируется взять кредит на некоторую сумму В июле 2020 года планируется взять кредит на некоторую сумму. Условия возврата таковы: — в январе каждого года долг увеличивается на 25% по сравнению с предыдущим годом; — с февраля по Читать далее …
Автор: Павел Коваленко
Реальный ЕГЭ 2го июня 2017, задание 16
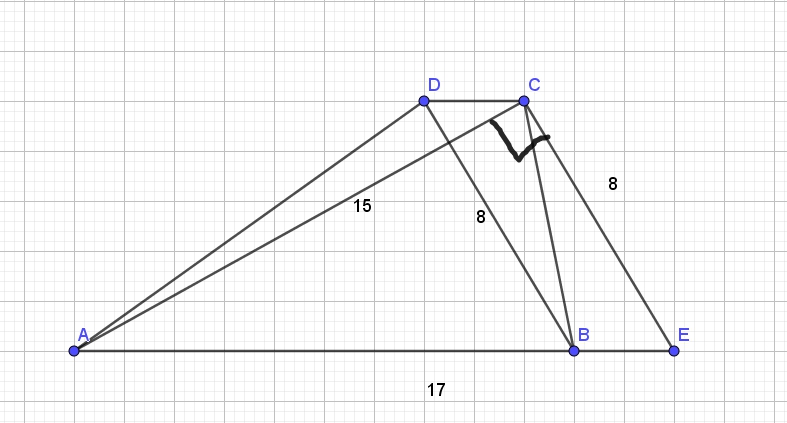
Дана трапеция ABCD с диагоналями равными 8 и 15. Сумма оснований трапеции равна 17. а) Докажите, что диагонали перпендикулярны. б) Найдите высоту трапеции Сделаем дополнительное построение — проведем . Тогда , а т.к. BECD — параллелограмм. В треугольнике ACE стороны Читать далее …
Реальный ЕГЭ 2го июня 2017, задание 14
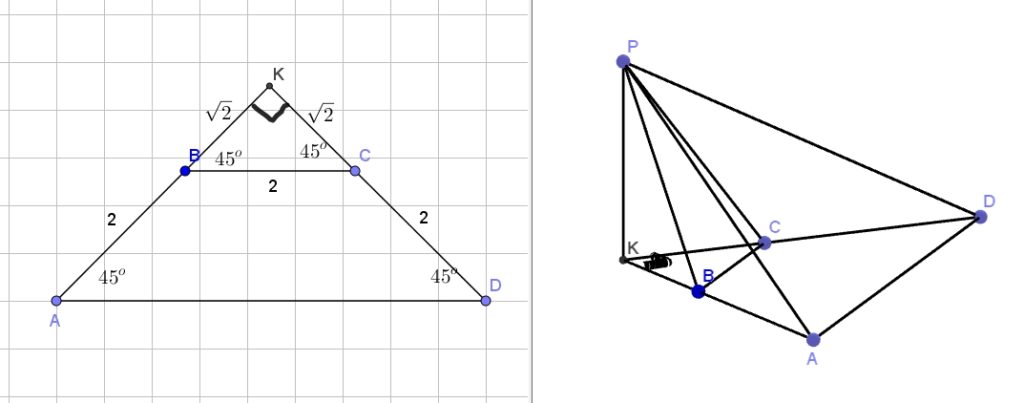
Дана пирамида PABCD, в основании которой трапеция ABCD большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K. а) Доказать, что плоскость Читать далее …
Реальный ЕГЭ 26го июня 2018, задание 15
Найдем ОДЗ: Логарифм по основанию 3 — возрастающая функция, значит: Пересекаем с ОДЗ выше и получаем ответ:
Реальный ЕГЭ 26го июня 2018, задание 14
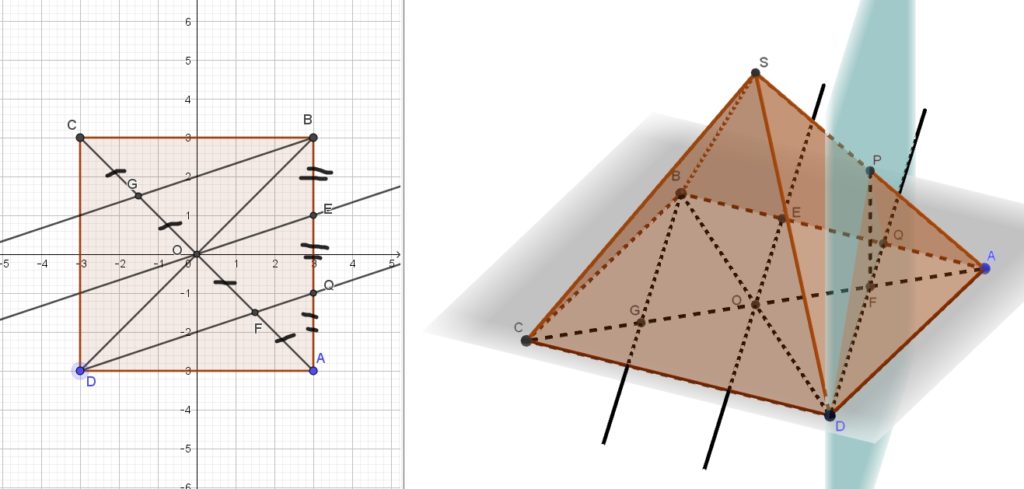
В правильной 4х-угольной пирамиде , -середина a) Докажите, что плоскость перпендикулярна плоскости основания b) Найдите площадь сечения если площадь =6 Проведем диагональ CA, поделим ее на 4 равные части. Возьмем на диагонали три равных отрезка . Возьмем на стороне три Читать далее …
Реальный ЕГЭ 26го июня 2018, задание 13
Реальный ЕГЭ 29 мая 2019, задание 18
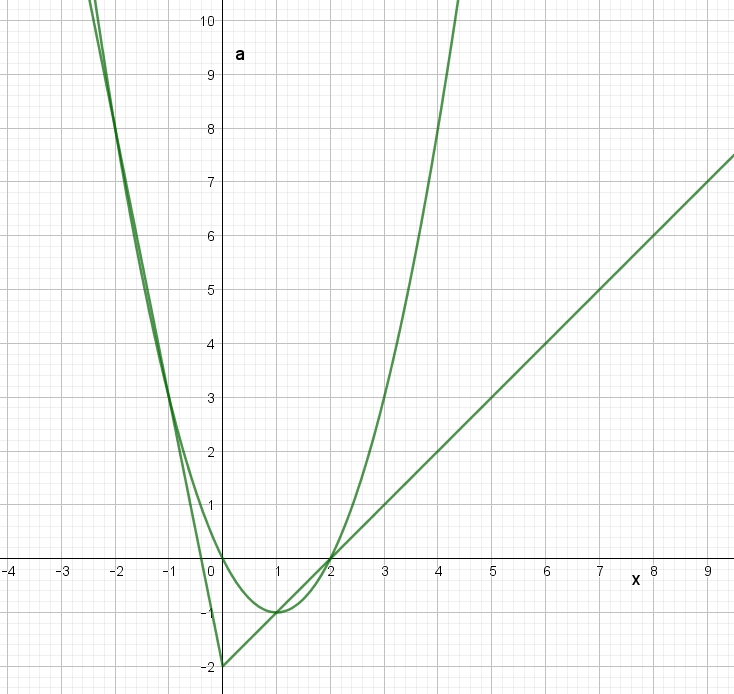
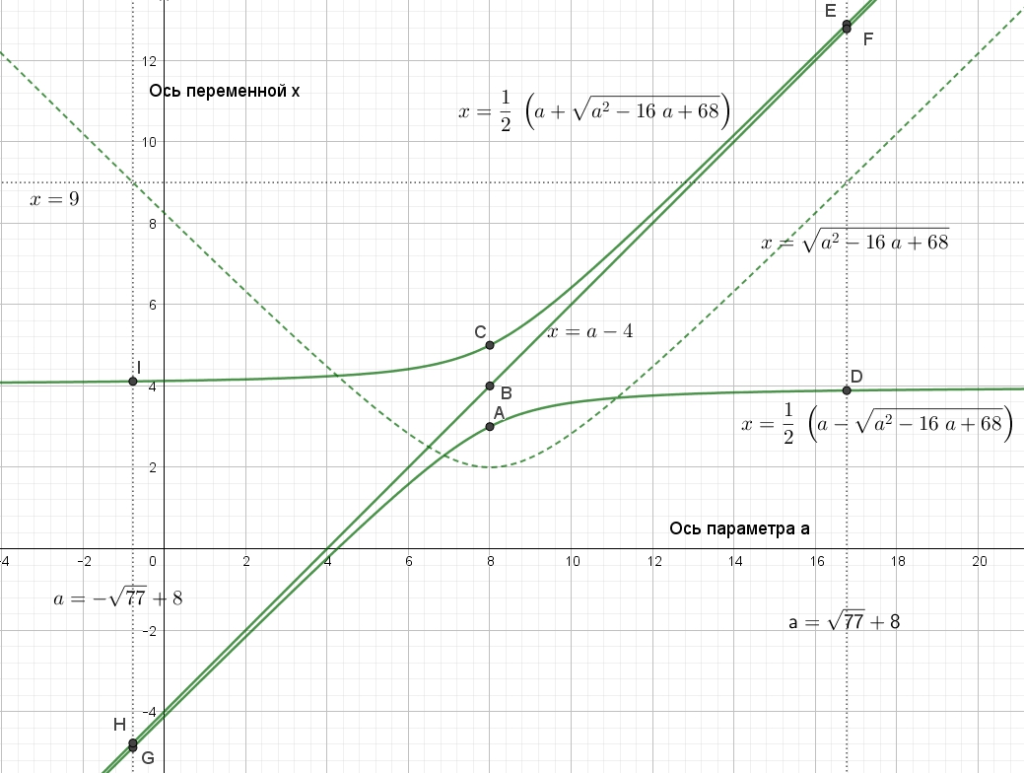
Найти все значения , при каждом из которых уравнение имеет ровно два различных корня. Решим систему уравнений безотносительно к количеству корней : или Нарисуем на плоскости (a;x) оба множества Первым множеством является все точки Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 17
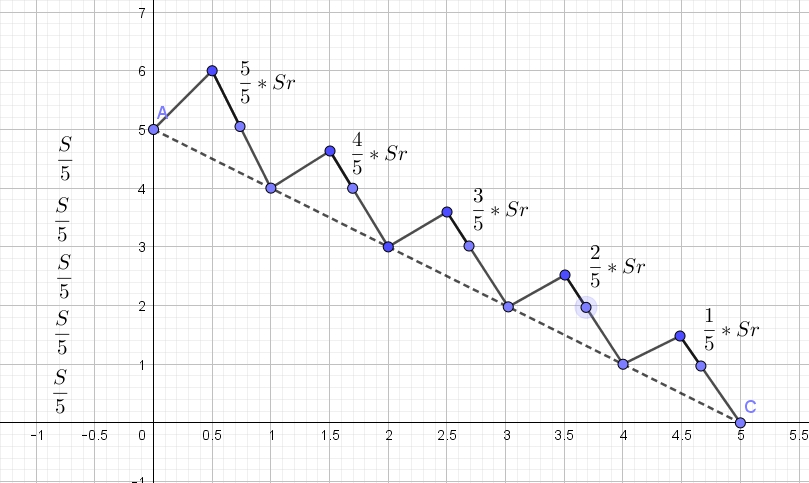
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 16
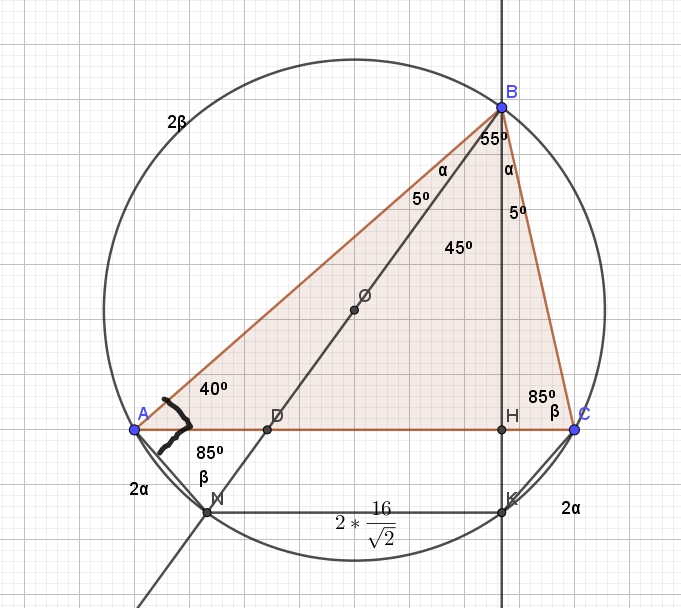
В остроугольном треугольнике ABC все стороны различны. Прямая, содержащая высоту BH треугольника ABC, вторично пересекает описанную около этого треугольника окружность в точке K. Отрезок BN — диаметр этой окружности. a) Докажите, что AN=CK b) Найдите NK, если радиус описанной около Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 15
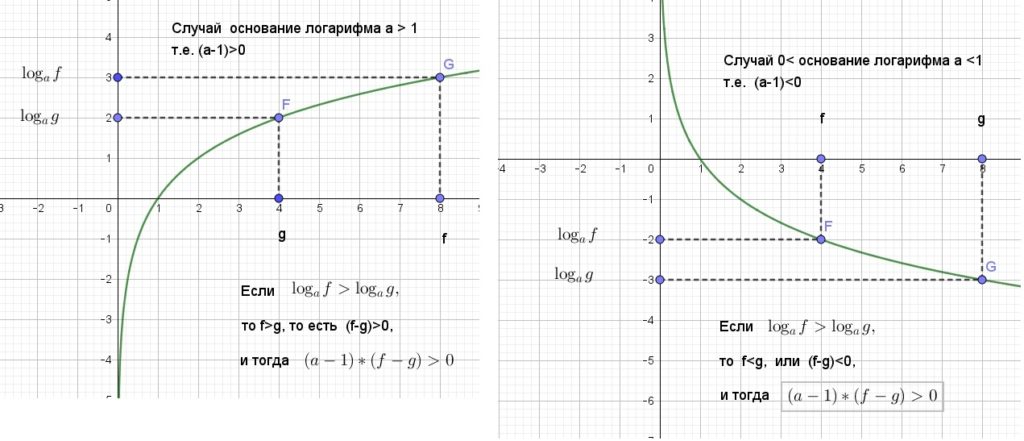
По методу замены множителей (см. учебник Ериной, стр 313 ) следующая функция будет иметь те же знаки на тех же интервалах (но каждая на своем ОДЗ): т.е. (1) Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 14

В правильной четырехугольной пирамиде сторона основания равна 6, а боковое ребро равно 7. На ребрах и отмечены точки и соответственно, причем . Плоскость содержит прямую и параллельна прямой . a) Докажите, что плоскость параллельна прямой b) Найдите расстояние от точки Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 13
Реальный ЕГЭ 29 мая 2019, задание 12
Найти точку минимума функции Найдем производную Нули производной и . Знаки производной на соответствующих интервалах: «плюс(+)» , -9, «минус(-)» ,9, «плюс(+)» Промежутки возрастания и убывания исходной функции Точка минимума
Реальный ЕГЭ 29 мая 2019, задание 11
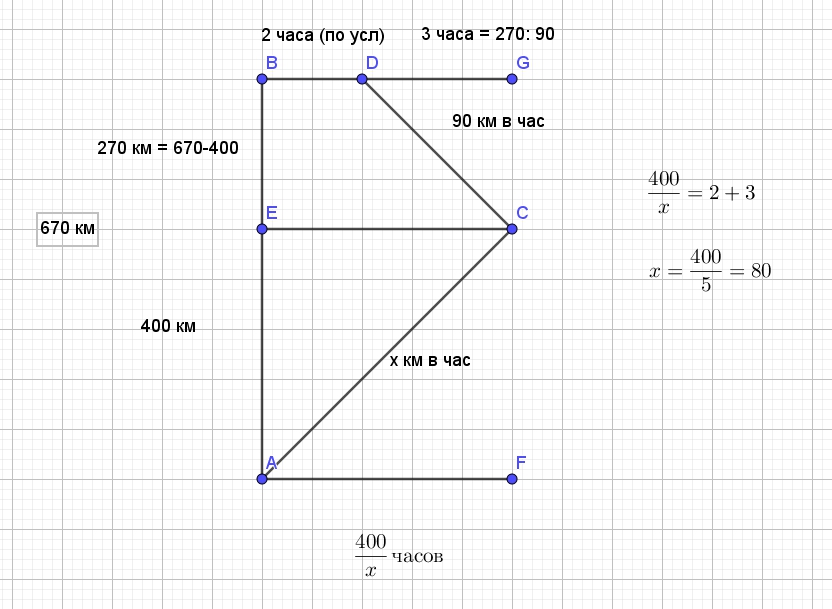
Расстояние между городами A и B равно 670 км. Из города A в город B выехал первый автомобиль, а через два часа после этого навстречу ему из города B выехал со скоростью 90 км/ч второй автомобиль. Найдите скорость первого автомобиля, Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 10
К источнику с ЭДС В и внутренним сопротивлением Ом, хотят подключить нагрузку с сопротивлением R Ом. Напряжение (в В) на этой нагрузке, вычисляется по формуле . При каком значении сопротивления нагрузки напряжение на ней будет не менее 50 В? Ответ Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 9
Найдите значение выражения Решение: Воспользуемся формулами 1,4, 5 и 6 логарифмов: https://ege-resheniya.ru/category/formuly-logarifmov
Реальный ЕГЭ 29 мая 2019, задание 8
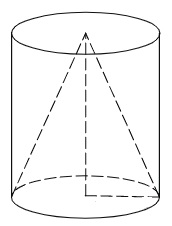
Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 6. Найдите объём цилиндра. Объем конуса: Объем цилиндра: Т.е. объем цилиндра в три раза больше, чем объем конуса с такими же и . Ответ: 18 Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 7
Вариант от Николая
Задача 8 Найти объем конуса, вписанного в шар объемом 36, если сечение конуса является равносторонним треугольником Задача 9 Найдите значение выражения Задача 12 Найдите наименьшее значение функции на отрезке Задача 13 Укажите корни этого Читать далее …
Решение задания 13, вариант 7, Ященко 36 вариантов, ЕГЭ-2019 (видео)
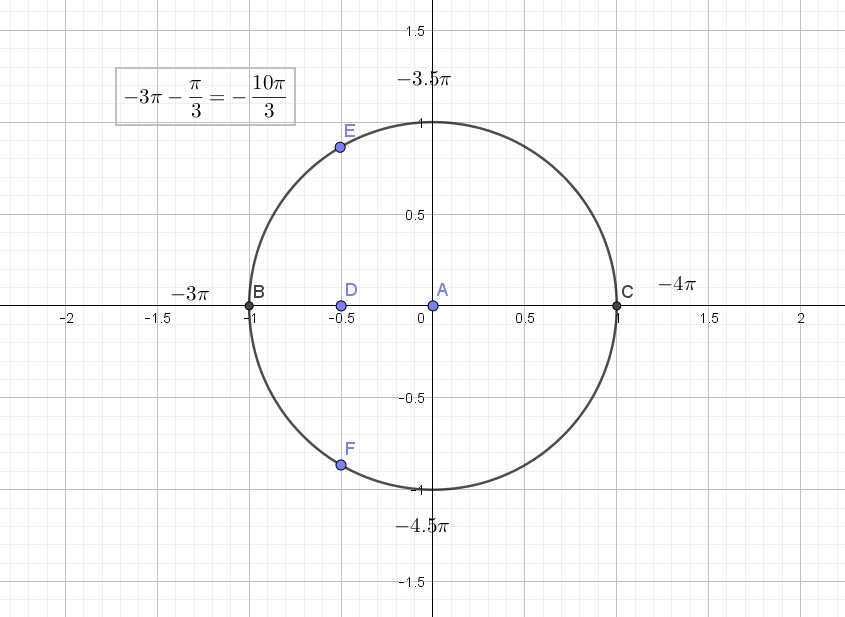
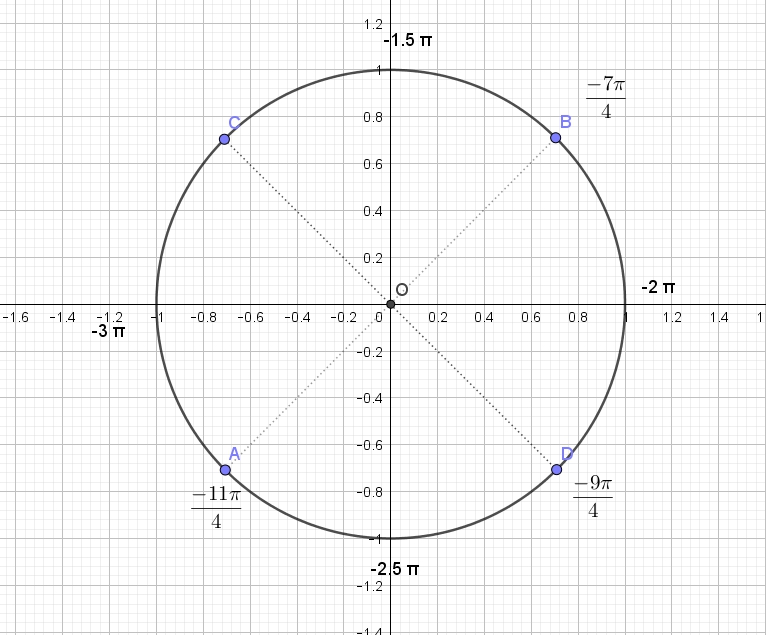
а) Решите уравнение 6) Найдите все корни этого уравнения, принадлежащие отрезку . Напишем ОДЗ: Когда произведение равно нулю? Когда либо одно, либо другое равно нулю: Решим первое уравнение: Читать далее …
Решение задания 17, вариант 3, Ященко 36 вариантов, ЕГЭ-2019
15-го июня планируется взять кредит в банке на сумму 1300 тысяч рублей на 16 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца; — со 2-го по 14-е Читать далее …
Решение задания 15, вариант 7, Ященко 36 вариантов, ЕГЭ-2019 (видео)
Решите неравенство (1) Напишем ОДЗ: (2) Пересечем (1) и (2), получим:
Интересные задачи по физике
https://phys-ege.sdamgia.ru/test?theme=305
книга Высоцкого стр 23 задача 18
задача 18 стр 23 Высоцкого При каких множество решений неравенств и совпадают? Решим первое неравенство при . при или 4. при =0: при : — неверно, таких нет. при : верно при любом при — т.е. при — Читать далее …
Задача 15
Здесь нужно воспользоваться формулой Тогда получится квадратное уравнение. Свойства функций и смотрите здесь
Задача 11
По плану одной бригаде нужно изготовить на 600 изделий больше,чем другой, за то же время. Чтобы каждая выполнила свой план на 2 дня раньше,в первую бригаду добавили 4 человека, а во вторую 3 человека. Сколько рабочих было в первой бригаде Читать далее …
Интересные видео по физике
Устройство и КПД электродвигателя: ссылка , ссылка , ссылка, ссылка
Записи вебинаров
Запись от 9го апреля. Решения 14х и 18х задач Запись от 12го марта. Решения 14х задач Запись от 5го марта. Что-то сломалось и экран не показывается 🙁 Запись от 26го февраля часть 2. Решения 14х задач. Запись от 26го Читать далее …
Таблица производных
Решение задания 18, вариант 36, Ященко 36 вариантов, ЕГЭ-2018
Делается по аналогии с вариантом 24
Решение задания 18, вариант 35, Ященко 36 вариантов, ЕГЭ-2018
Найдите все значения , при каждом из которых неравенство выполняется для всех значений . Перепишем Заметим, что слева — убывающая по функция, как бы ни раскрывались модули. Значит максимум у нее в левом конце отрезка . Читать далее …
Решение задания 18, вариант 34, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 33, Ященко 36 вариантов, ЕГЭ-2018
Найдите все значения , при каждом из которых неравенство выполняется для всех значений . Перепишем Заметим, что слева — убывающая по функция, как бы ни раскрывались модули. Значит максимум у нее в левом конце отрезка . Читать далее …
Решение задания 18, вариант 32, Ященко 36 вариантов, ЕГЭ-2018
Решение есть в самой книжке Лысенко на стр.250. Посмотрите там (нажмите на ссылку).
Решение задания 18, вариант 31, Ященко 36 вариантов, ЕГЭ-2018
Делается по аналогии с вариантом 23
Решение задания 18, вариант 30, Ященко 36 вариантов, ЕГЭ-2018
Найдите все значения , при каждом из которых уравнение имеет хотя бы одно решение на отрезке . Заметим, что на отрезке функция , т.е. точно . Заметим также, что отсюда сразу следует, что , т.к. если бы оно Читать далее …
Решение задания 18, вариант 29, Ященко 36 вариантов, ЕГЭ-2018
Найдите все значения , при каждом из которых уравнение имеет хотя бы один корень. Перепишем уравнение в виде Заметим, что слева стоит функция четных степеней, симметричная относительно оси , а справа — функция нечетных, симметричная относительно замены на . Как Читать далее …
Решение задания 18, вариант 28, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 27, Ященко 36 вариантов, ЕГЭ-2018
Решение есть в самой книжке Лысенко на стр.243. Посмотрите там (нажмите на ссылку).
Решение задания 18, вариант 26, Ященко 36 вариантов, ЕГЭ-2018
Делается по аналогии с вариантом 23