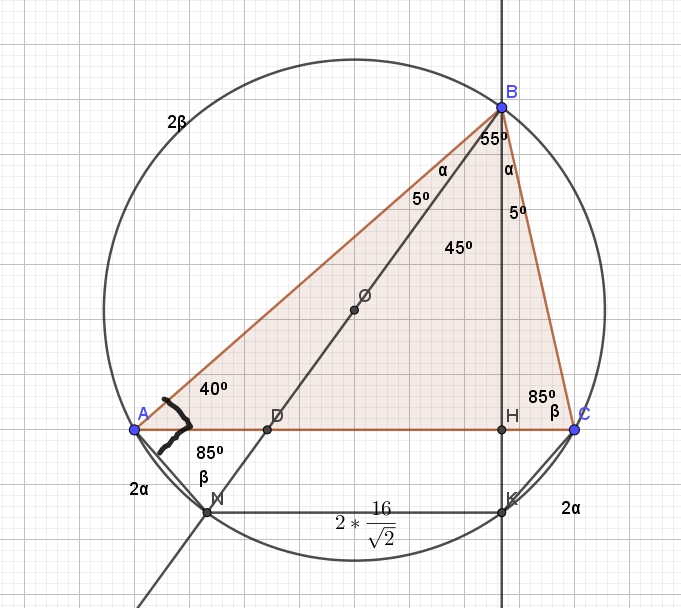
Реальный ЕГЭ 29 мая 2019, задание 16 — Решения вариантов ЕГЭ по математике

В остроугольном треугольнике ABC все стороны различны. Прямая, содержащая высоту BH треугольника ABC, вторично пересекает описанную около этого треугольника окружность в точке K. Отрезок BN — диаметр этой окружности.
a) Докажите, что AN=CK
b) Найдите NK, если радиус описанной около треугольника ABC окружности равен 16 , $\angle BAC=40^o, \angle ACB=85^o$

Обозначим в прямоугольном треугольнике BHC углы буквами $\alpha$ и $\beta$ . Заметим, что $\alpha+ \beta=90^o$ .
Заметим, что $\angle ACB$ (который $\beta$ ) $=\angle ANB$ , как опирающийся на ту же дугу $AB=2\beta$
Но т.к. $\angle NAB=90^o$ (опирается на диаметр), то $\angle ABN = 90-\beta = \alpha$ и тогда хорды AN и KC равны, как хорды одинаковых углов $\alpha$ .

Часть 2.
Т.к. $\beta=85^o$ по условию, то $\alpha=5^o$ .
$\angle ABC=180-40-85=55^o$
$\angle NBK=55-\alpha-\alpha=55-5-5=45^o$
Треугольник BNK — прямоугольный (BN — диаметр=32 = 2 радиуса по 16), с одним углом 45, значит второй угол тоже 45 градусов. Тогда $NK=\frac{BN}{\sqrt{2}}=\frac{32}{\sqrt{2}}=16\sqrt{2}$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru