задача 12 задача 11 задача 10 задача 9 задача 8 задача 13
14е задачи
Рубрика: Задание 14 (стереометрия)
Решение задания 14.15, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
Подготовительные задания, стр. 128 15. Ребро SА пирамиды SАВС перпендикулярно плоскости основания АВС. а) Докажите, что плоскость, проходящая через середины рёбер АВ, АС и SА, параллельна плоскости SВС. 6) Найдите расстояние от вершины А до этой плоскости, если SА = Читать далее …
Решение задания 14.14, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
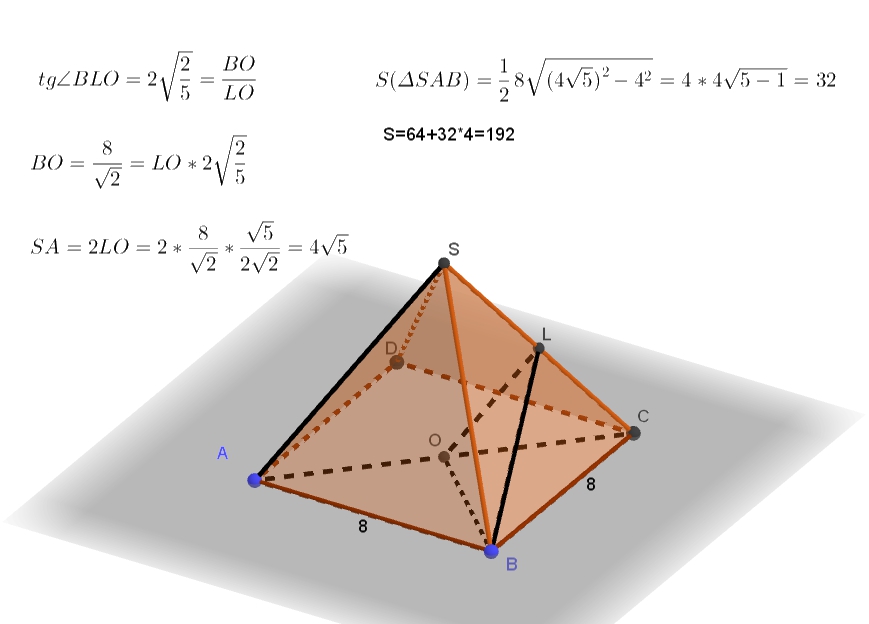
Подготовительные задания, стр. 128 14. В правильной четырёхугольной пирамиде SАВСD с вершиной S сторона основания равна 8. Точка L — середина ребра SC. Тангенс угла между прямыми ВL и SА равен . а) Пусть О — центр основания пирамиды. Докажите, Читать далее …
Решение задания 14.13, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
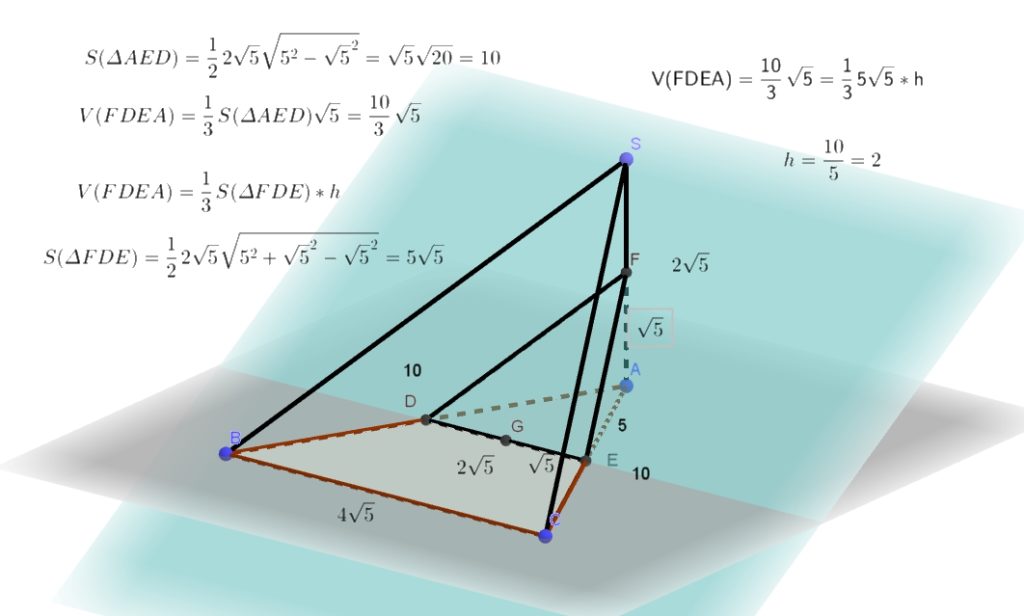
Подготовительные задания, стр. 128 13. В правильной треугольной пирамиде SАВС с вершиной S, все рёбра которой равны 6, точ- ка М — середина ребра ВС, точка О — центр основания пирамиды, точка F делит отрезок SО в отношении 1:2, считая Читать далее …
Решение задания 14.12, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
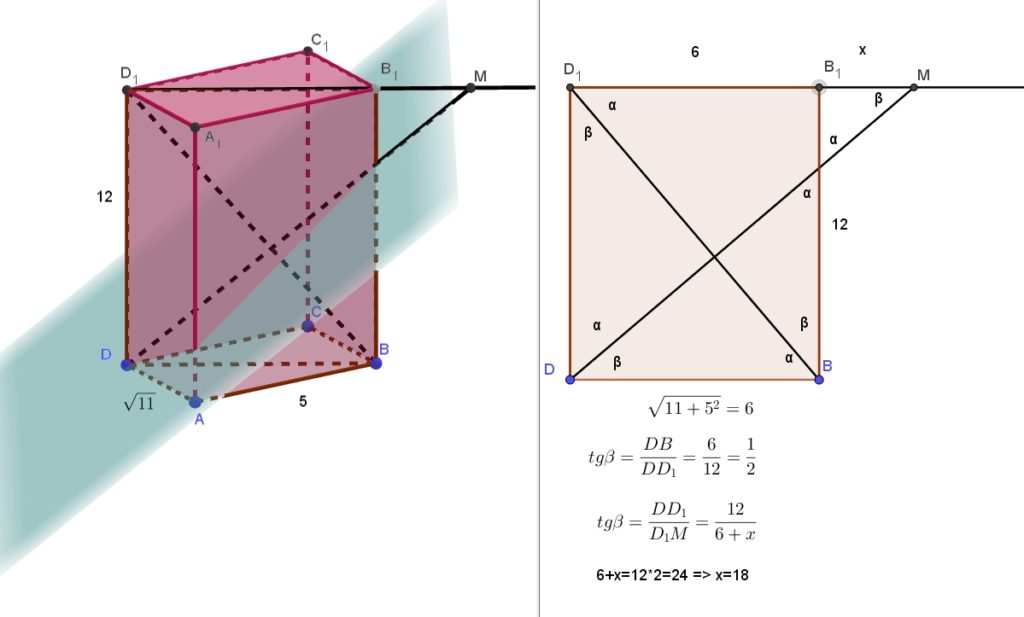
Подготовительные задания, стр. 128 12. Основание прямой четырёхугольной призмы АВСDА1В1С1D1 — прямоугольник АВСD, в котором АВ = 5, AD = . Расстояние между прямыми АС и B1D1, равно 12. а) Пусть плоскость, проходящая через точку D перпендикулярно прямой ВD1 пересекает Читать далее …
Решение задания 14.11, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
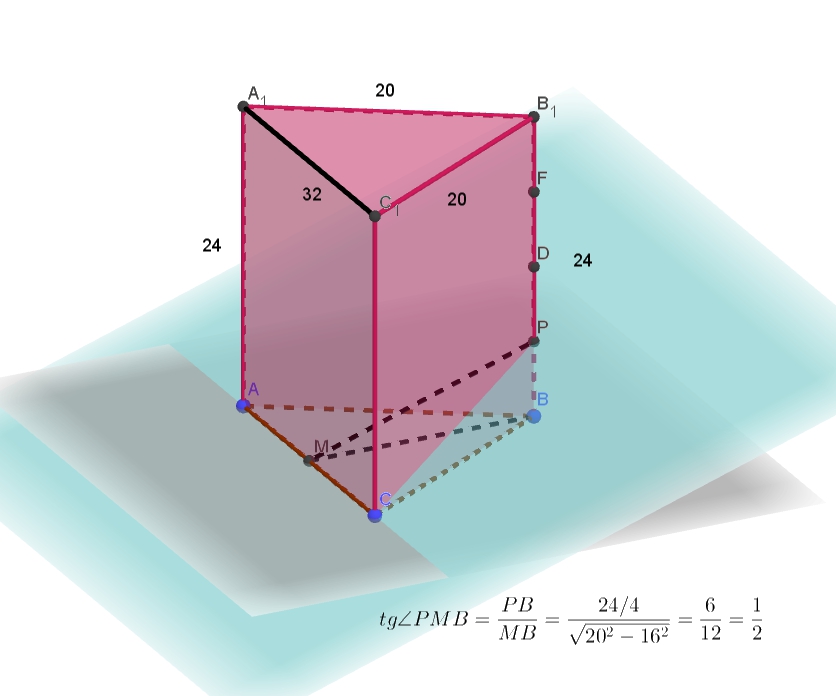
Подготовительные задания, стр. 128 11. Основанием прямой треугольной призмы АВСА1В1С1, является равнобедренный треуголь- ник АВС, в котором АВ = ВС = 20, АС = 32. Боковое ребро призмы равно 24. Точка Р при- надлежит ребру ВВ1, причём ВР:РВ1 =1:3. а) Читать далее …
Решение задания 14.10, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
Подготовительные задания, стр. 128 10. Дан куб ABCDA1B1C1D1. а) Докажите, что сечение куба плоскостью, проходящей через центр куба перпендику- лярно диагонали AC1, является правильным шестиугольником. 6) Найдите угол между прямой АС1, и плоскостью ВСС1.
Решение задания 14.9, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
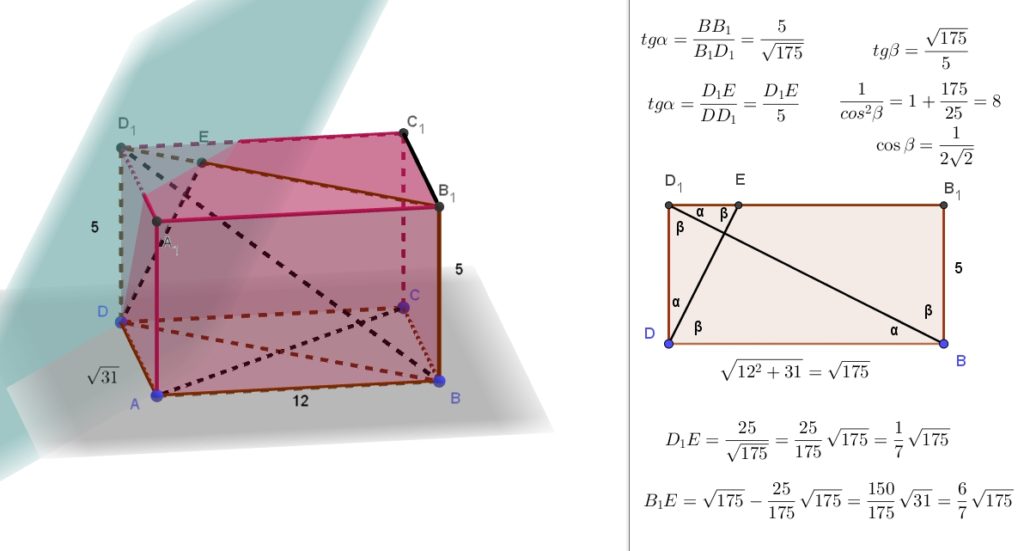
Подготовительные задания, стр. 128 9. Основание прямой четырёхугольной призмы АВСDА1В1С1D1, — прямоугольник АВСD, в котором АВ = 12, АD = . Расстояние между прямыми АС и B1D1, равно 5. а) Докажите, что плоскость, проходящая через точку D перпендикулярно прямой ВD1, Читать далее …
Решение задания 14.8, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
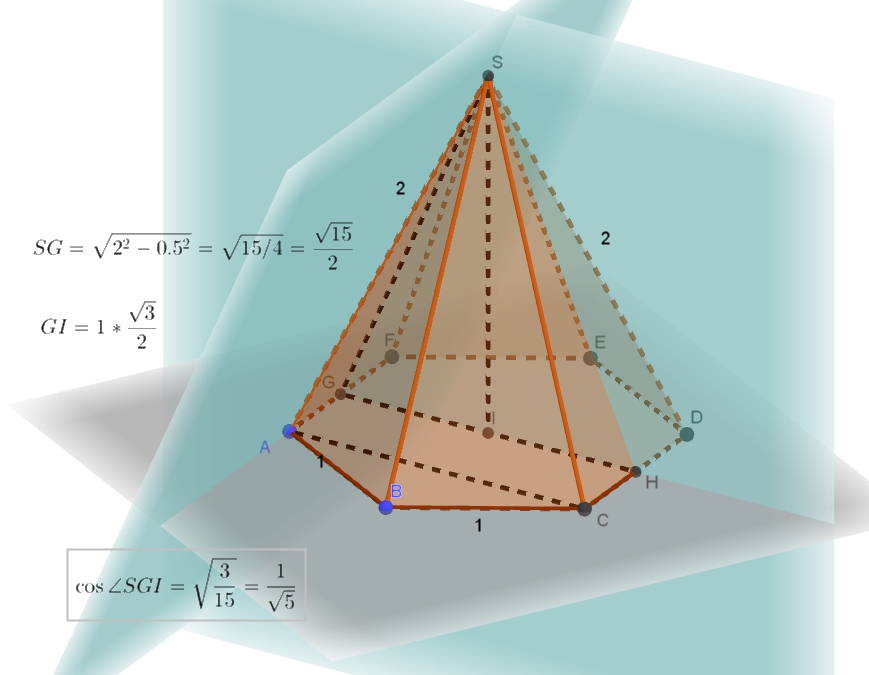
Подготовительные задания, стр. 128 8. В правильной шестиугольной пирамиде SАВСDЕF боковые рёбра равны 2, а стороны ос- нования — 1. а) Докажите, что плоскость, проходящая через вершину S и середины рёбер АF и СD, пер- пендикулярна плоскости основания. 6) Найдите Читать далее …
Решение задания 14.7, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
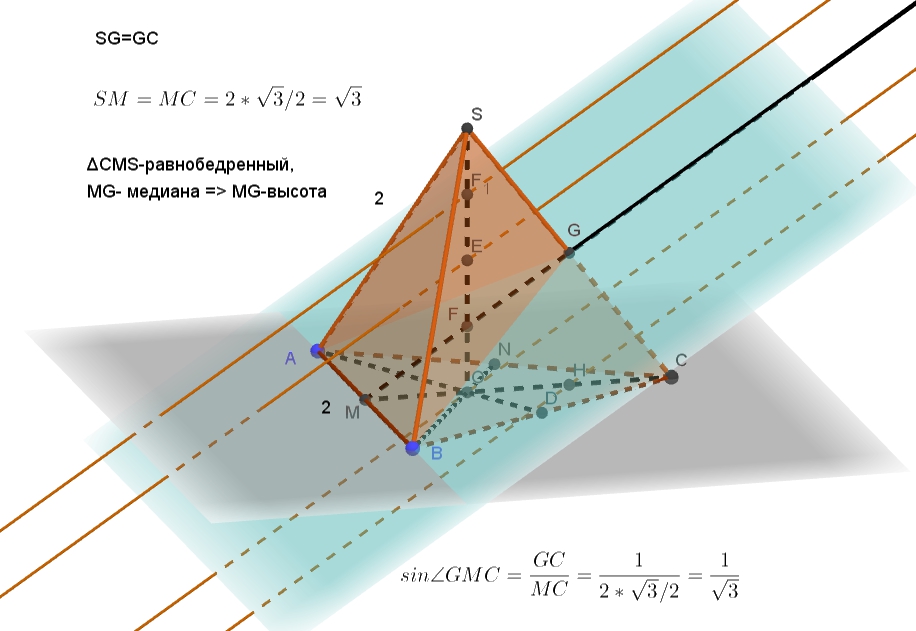
Подготовительные задания, стр. 128 7. В правильной треугольной пирамиде SАВС с вершиной S, все рёбра которой равны 2, точ- ка М — середина ребра АВ, точка О — центр основания пирамиды, точка F делит отрезок SО в отношении 3 : Читать далее …
Решение задания 14.6, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
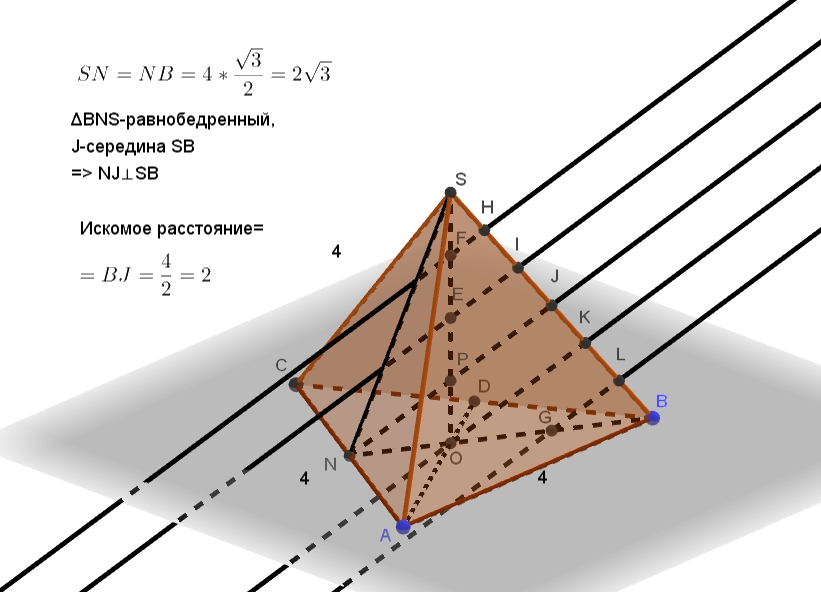
Подготовительные задания, стр. 128 6. В правильной треугольной пирамиде SABC с вершиной S, все рёбра которой равны 4, точ- ка N — середина ребра АС, точка О — центр основания пирамиды, точка Р делит отрезок SO вотношении 3:1, считая от Читать далее …
Решение задания 14.5, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
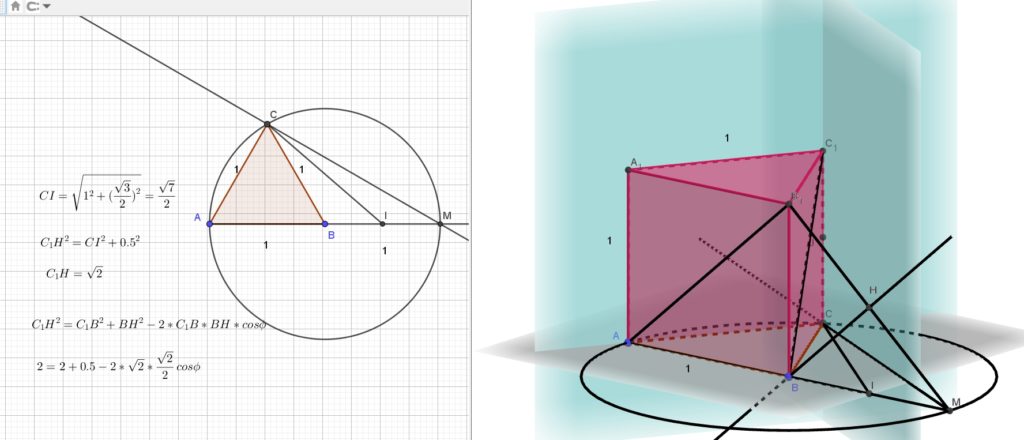
Подготовительные задания, стр. 128 5. В правильной треугольной призме АВСA1B1C1, все рёбра равны 1. а) Пусть плоскость, проходящая через точки С, С1 перпендикулярно плоскости АСС1, пе- ресекает прямую АВ вточке М. Докажите, что треугольник МВВ1 равнобедренный. 6) Найдите косинус угла Читать далее …
Решение задания 14.4, Ященко 20 вариантов, ЕГЭ-2019, тематическая рабочая тетрадь
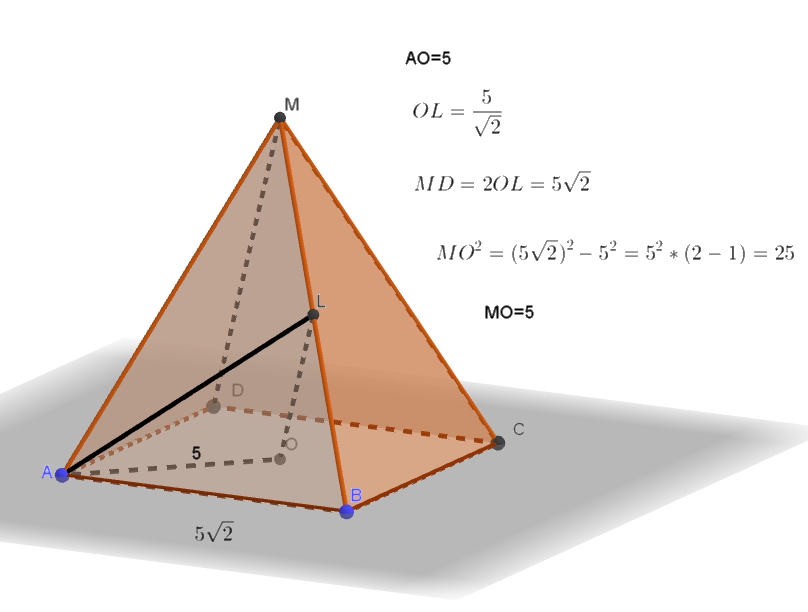
Подготовительные задания, стр. 128 4. Дана правильная четырёхугольная пирамида MABCD, рёбра основания которой равны . Точка L — середина ребра МВ. Тангенс угла между прямыми DM и AL равен . а) Пусть О — центр основания пирамиды. Докажите, что прямые Читать далее …
Решение задания 14.3, Ященко 20 вариантов, ЕГЭ-2019, подготовительные задания, стр. 128
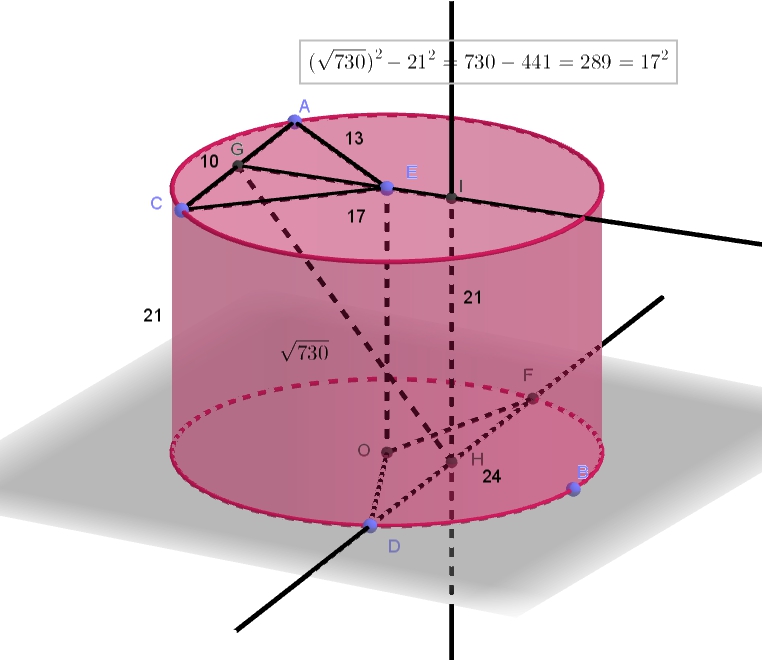
3. Диаметр окружности основания цилиндра равен 26, образующая цилиндра равна 21. Плоскость пересекает его основания по хордам длины 24 и 10. Расстояние между этими хордами равно . а) Докажите, что эта плоскость пересекает ось цилиндра. 6) Найдите угол между этой Читать далее …
Решение задания 14.2, Ященко 20 вариантов, ЕГЭ-2019, подготовительные задания, стр. 128
2. Площадь основания правильной четырёхугольной пирамиды SABCD равна 64. а) Докажите, что плоскость, проходящая через вершину S и середины рёбер ВС и АD, со- держит высоту пирамиды. 6) Найдите площадь боковой поверхности этой пирамиды, если площадь сечения пирами- ды плоскостью Читать далее …
Решение задания 14.1, Ященко 20 вариантов, ЕГЭ-2019, подготовительные задания
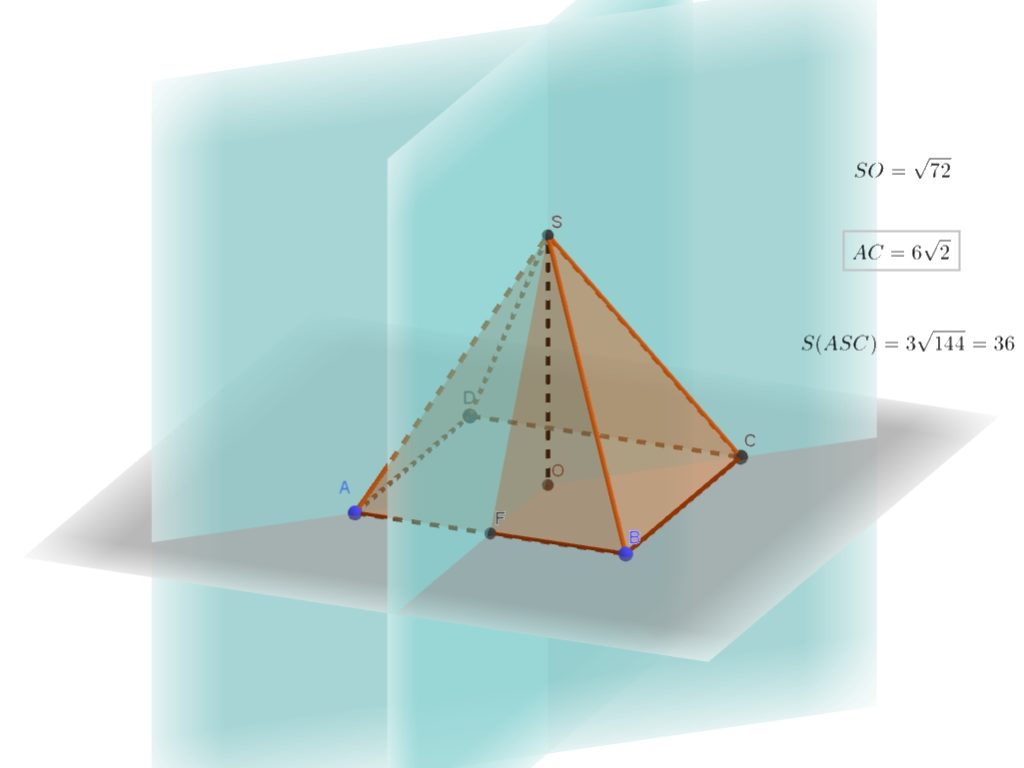
1. Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108, а площадь полной поверхности этой пирамиды равна 144. а) Докажите, что плоскость SAC и плоскость, проходящая через вершину S, середину сто- роны АВ и центр основания, пересекаются по прямой, содержащей Читать далее …
Решение задания 14, вариант 7, Ященко 36 вариантов, ЕГЭ-2019 (видео)
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания — точка С, причём СС1, — образующая цилиндра, а АС — диаметр основания. Известно, что угол АСВ=45°, Читать далее …
Реальный ЕГЭ 2го июня 2017, задание 14
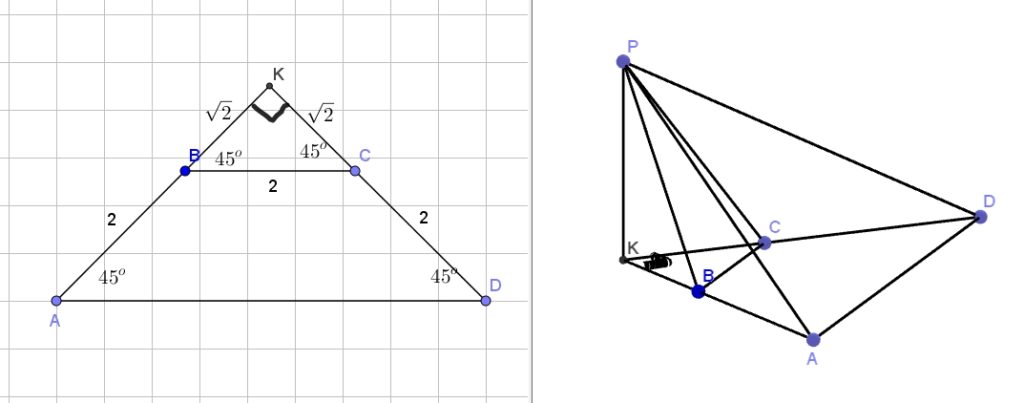
Дана пирамида PABCD, в основании которой трапеция ABCD большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K. а) Доказать, что плоскость Читать далее …
Реальный ЕГЭ 26го июня 2018, задание 14
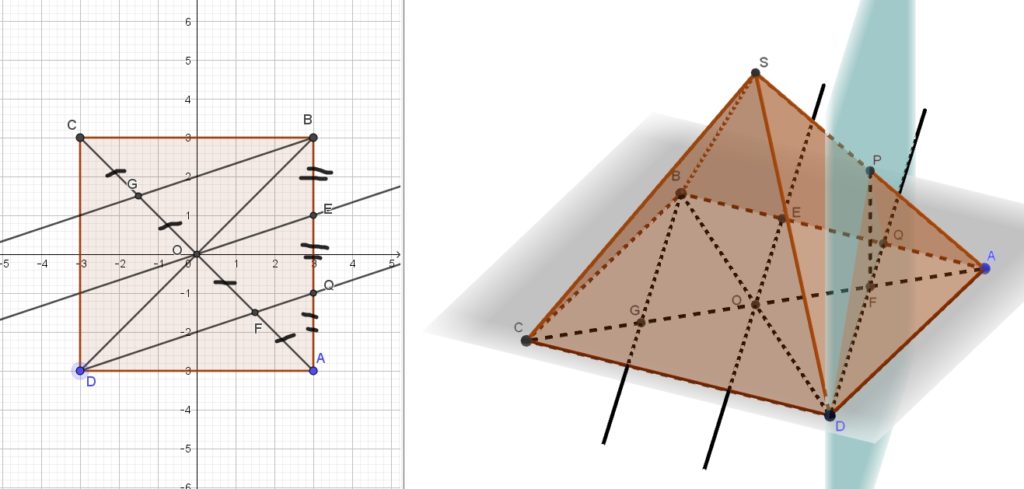
В правильной 4х-угольной пирамиде , -середина a) Докажите, что плоскость перпендикулярна плоскости основания b) Найдите площадь сечения если площадь =6 Проведем диагональ CA, поделим ее на 4 равные части. Возьмем на диагонали три равных отрезка . Возьмем на стороне три Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 14
В правильной четырехугольной пирамиде сторона основания равна 6, а боковое ребро равно 7. На ребрах и отмечены точки и соответственно, причем . Плоскость содержит прямую и параллельна прямой . a) Докажите, что плоскость параллельна прямой b) Найдите расстояние от точки Читать далее …
Решение задания 14, вариант 36, Ященко 36 вариантов, ЕГЭ-2018
В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 5. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что AD = Читать далее …
Решение задания 14, вариант 35, Ященко 36 вариантов, ЕГЭ-2018
На рисунке изображён многогранник, все двугранные углы которого прямые. а) Постройте сечение многогранника плоскостью, проходящей через точки А, В и С1 б) Найдите площадь этого сечения. Решается аналогично как здесь
Решение задания 14, вариант 34, Ященко 36 вариантов, ЕГЭ-2018
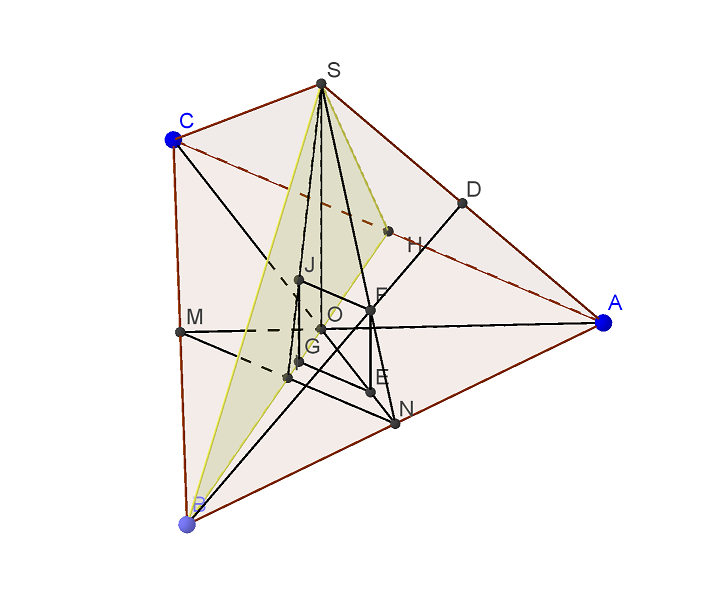
В правильной треугольной пирамиде SABC с основанием ABC все ребра равны 6. а) Постройте сечение пирамиды плоскостью, проходящей через вершину S и перпендикулярной отрезку, соединяющему середины ребер AB и BC. б) найдите расстояние от плоскости этого сечения до центра грани Читать далее …
Решение задания 14, вариант 33, Ященко 36 вариантов, ЕГЭ-2018
Похоже на решение вариантов 22 и 29. Посмотрите решение в варианте 22.
Решение задания 14, вариант 32, Ященко 36 вариантов, ЕГЭ-2018
В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 8. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что CD = Читать далее …
Решение задания 14, вариант 31, Ященко 36 вариантов, ЕГЭ-2018
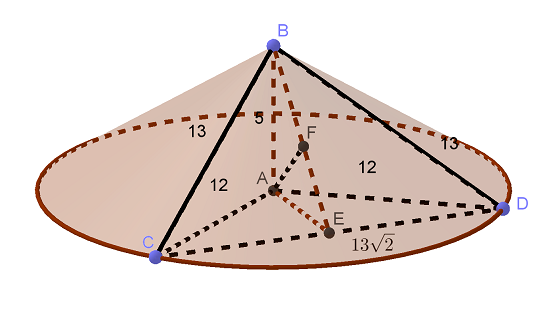
Радиус основания конуса равен 12, а высота конуса равна 5. а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие. б) Найдите расстояние от плоскости сечения до центра основания конуса. Трехмерная картинка, которую можно крутить в 3D, Читать далее …
Решение задания 14, вариант 30, Ященко 36 вариантов, ЕГЭ-2018
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 6. Длины боковых рёбер пирамиды SA = 3, SB = 5, SD = . а) Докажите, что SA — высота пирамиды. б) Найдите расстояние Читать далее …
Решение задания 14, вариант 29, Ященко 36 вариантов, ЕГЭ-2018
Вокруг куба с ребром 3 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …
Решение задания 14, вариант 28, Ященко 36 вариантов, ЕГЭ-2018
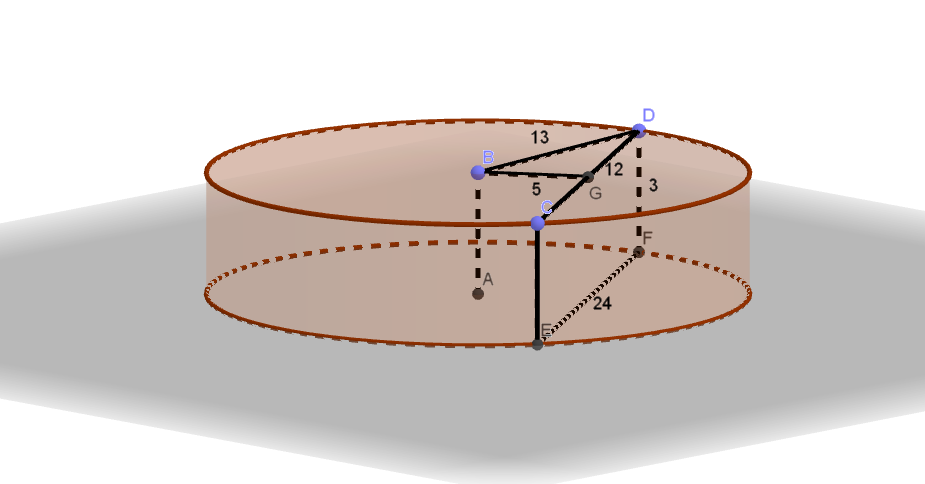
Высота цилиндра равна 3, а радиус основания равен 13. а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72. б) Найдите расстояние от плоскости сечения до центра основания цилиндра. Трехмерная картинка, которую можно крутить Читать далее …
Решение задания 14, вариант 27, Ященко 36 вариантов, ЕГЭ-2018
В кубе все рёбра равны 4. На его ребре отмечена точка K так, что KB=3. Через точки K и проведена плоскость α, параллельная прямой . а) Докажите, что , где Р — точка пересечения плоскости α с ребром . б) Читать далее …
Решение задания 14, вариант 26, Ященко 36 вариантов, ЕГЭ-2018
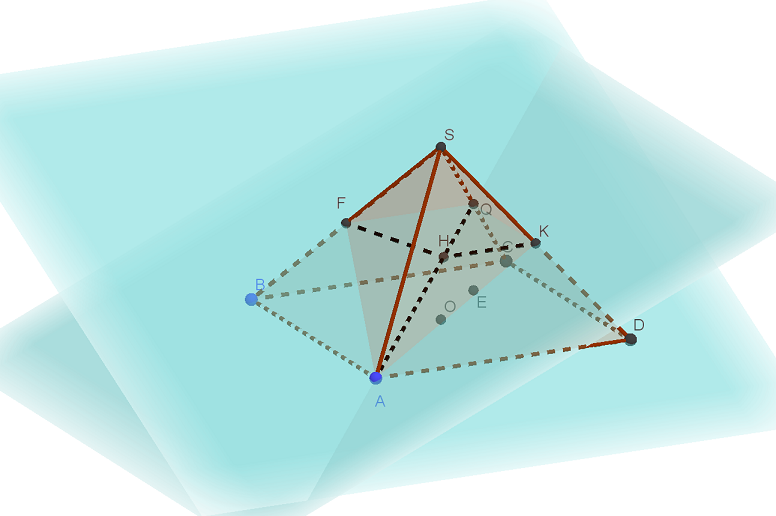
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, G(она же Q) — середина ребра SC. а) Постройте прямую пересечения плоскостей ABQ и QDF. б) Найдите угол между плоскостями ABQ и QDF. Трехмерная картинка, Читать далее …
Решение задания 14, вариант 25, Ященко 36 вариантов, ЕГЭ-2018
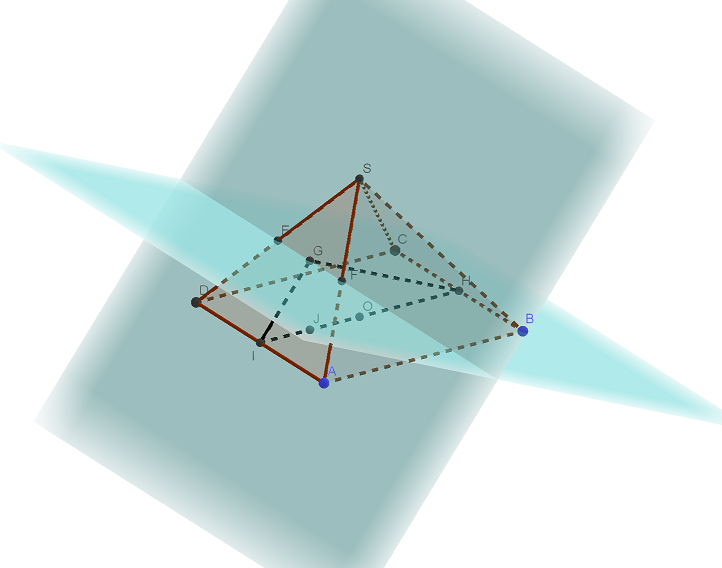
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра AS. а) Постройте прямую пересечения плоскостей SAD и BCF. б) Найдите угол между плоскостями SAD и BCF. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …
Решение задания 14, вариант 24, Ященко 36 вариантов, ЕГЭ-2018
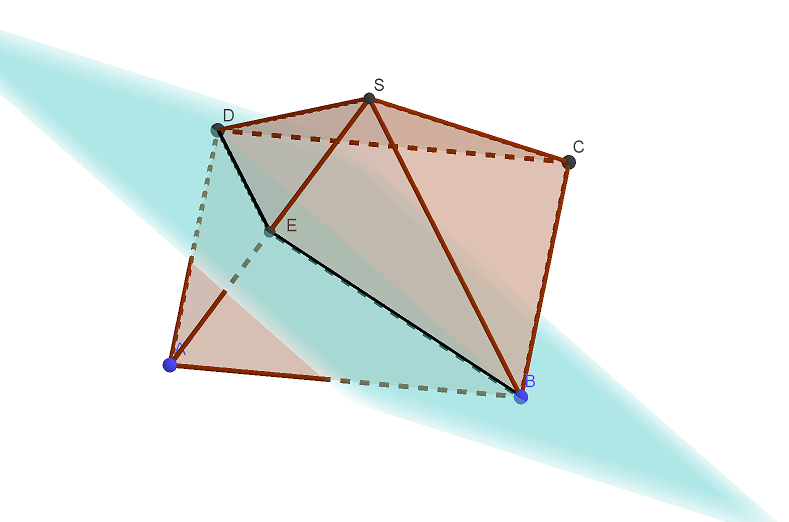
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. а) Постройте прямую пересечения плоскости SAD с плоскостью, проходящей через точку В перпендикулярно прямой AS. б) Найдите угол между плоскостью SAD и плоскостью, проходящей через точку В перпендикулярно прямой AS. Трехмерная Читать далее …
Решение задания 14, вариант 23, Ященко 36 вариантов, ЕГЭ-2018
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 3. Длины боковых рёбер пирамиды SA = √11 , SB = 3√3, SD = 2√5. а) Докажите, что SA — высота пирамиды. б) Найдите Читать далее …
Решение задания 14, вариант 22, Ященко 36 вариантов, ЕГЭ-2018
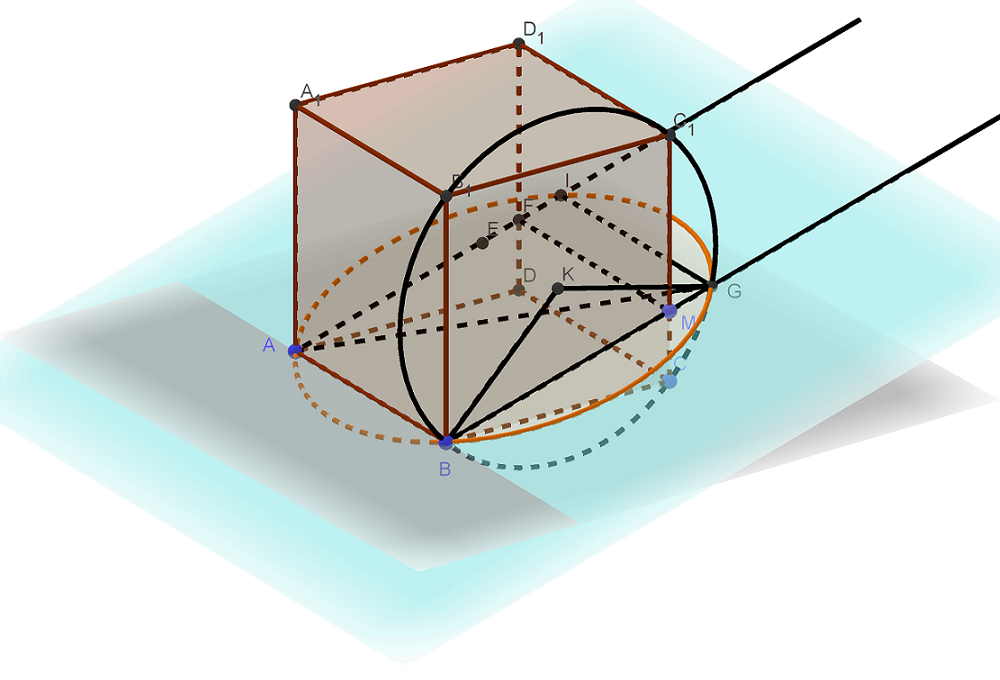
Вокруг куба с ребром 2 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …
Решение задания 14, вариант 21, Ященко 36 вариантов, ЕГЭ-2018
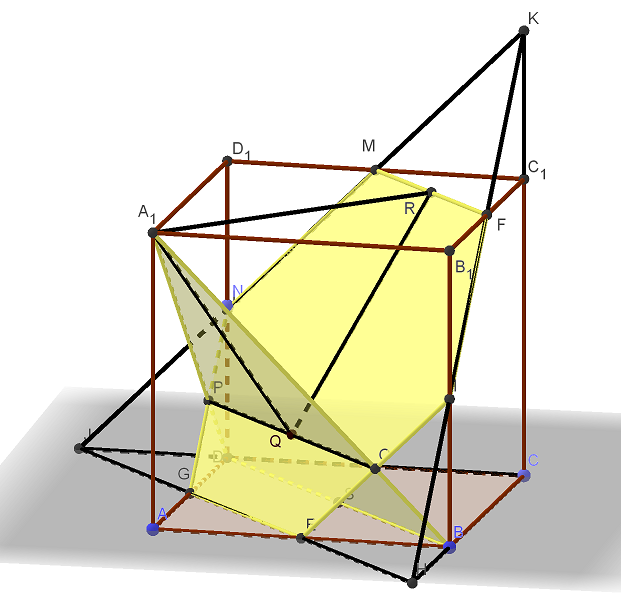
Дан куб . а) Постройте сечение куба плоскостью, проходящей через середины его рёбер . б) Найдите угол между плоскостью и плоскостью, проходящей через середины рёбер . Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/nAKXHwEB Пусть — ребро Читать далее …
Решение задания 14, вариант 20, Ященко 36 вариантов, ЕГЭ-2018
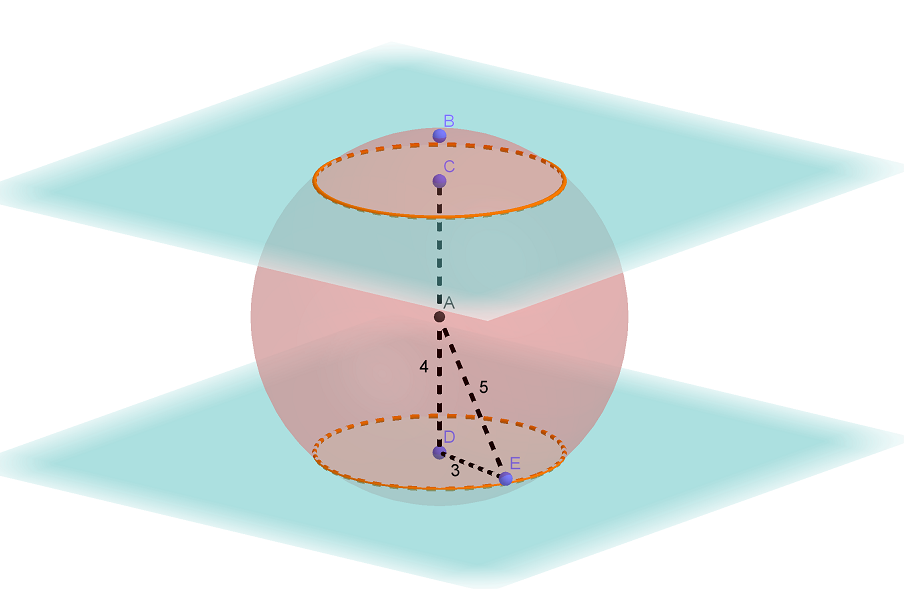
Две параллельные плоскости, находящиеся на расстоянии 8 друг от друга, пересекают шар. Получившиеся сечения одинаковы, и площадь каждого из них равна 9π. а) Постройте эти сечения. б) Найдите площадь поверхности шара. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …
Решение задания 14, вариант 19, Ященко 36 вариантов, ЕГЭ-2018
В правильной треугольной пирамиде SABC сторона основания АВ равна 60, а боковое ребро SA равно 37. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
Решение задания 14, вариант 18, Ященко 36 вариантов, ЕГЭ-2018
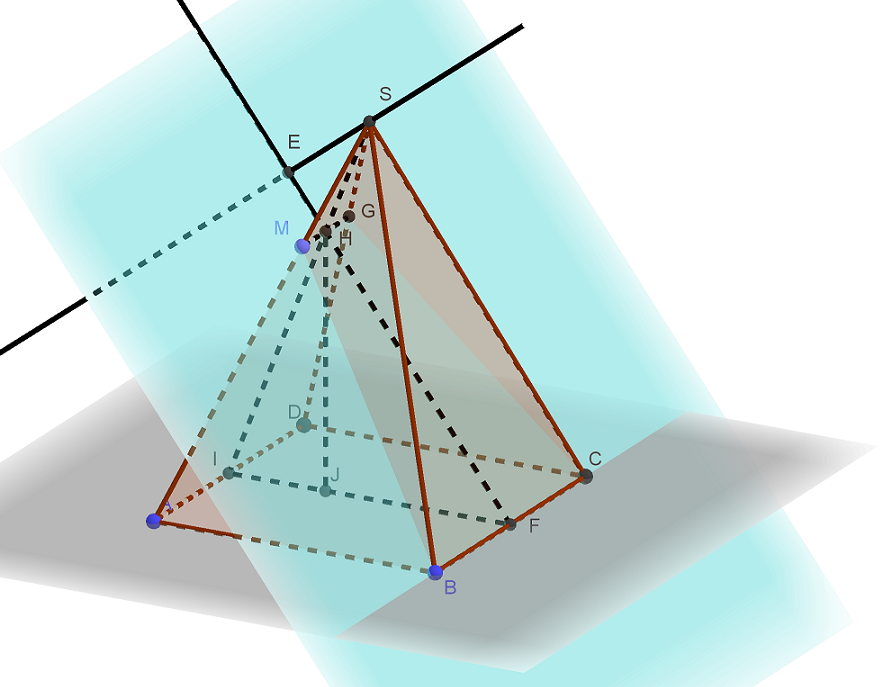
В правильной четырёхугольной пирамиде SABCD основание ABCD — квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что AM = 6. а) Постройте перпендикуляр из точки S на плоскость ВСМ. б) Найдите расстояние Читать далее …
Решение задания 14, вариант 17, Ященко 36 вариантов, ЕГЭ-2018
Дан куб . а) Постройте сечение куба плоскостью, проходящей через точки и . б) Найдите угол между плоскостями и . Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/mVj9KVSX