Реальный ЕГЭ 2го июня 2017, задание 14

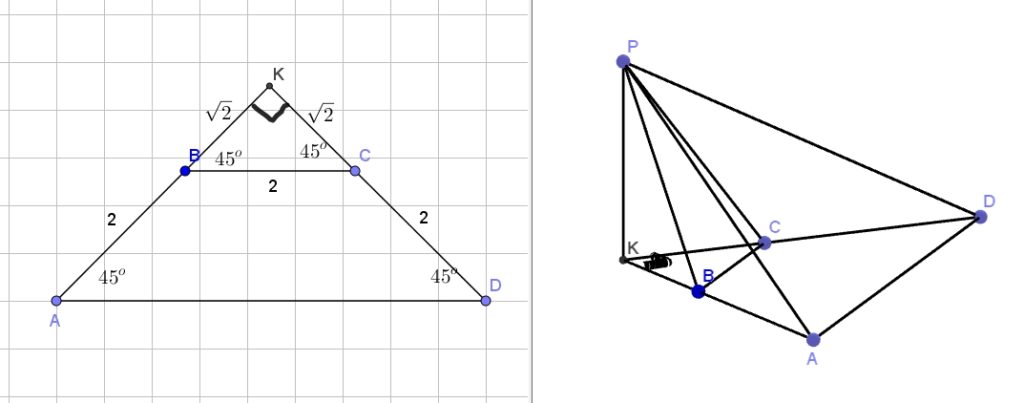
Дана пирамида PABCD, в основании которой трапеция ABCD большим основанием AD. Известно, что сумма углов BAD и ADC равна 90 градусов, а плоскости PAB и PCD перпендикулярны основанию, прямые AB и CD пересекаются в точке K.

а) Доказать, что плоскость PAB перпендикулярна плоскости PCD.

б) Найдите объём PKBC, если AB = BC = CD = 2, а высота пирамиды PABCD = 12.

Плоскости PAB и PCD пересекаются по некоторой прямой, причем точка P лежит на этой прямой, т.к. она лежит в обоих плоскостях. Прямые AB и CD лежат в плоскостях PAB и PCD соответственно, и т.к. они пересекаются в т. K, то точка K также лежит в обоих плоскостях PAB и PCD. Но тогда прямая PK есть прямая пересечения этих плоскостей.
Предположим, что PK не перпендикулярна плоскости основания (ABC), тогда PK есть наклонная (под каким-то углом к основанию меньшим 90 градусов) и тогда угол между плоскостью основания и плоскостью, которая проходит через PK будет тем же самым и меньшим 90 градусов — это легко видно, если вспомнить определение угла между плоскостями. А у нас через PK проходят обе плоскости (PAB)и (PCD) и мы знаем, что они обе перпендикулярны основанию. Получили противоречие. Значит плоскости основания и является высотой пирамиды PABCD.
и
Но так как сумма углов BAD и ADC равна 90 градусов, то угол AKD = 90 градусов.
Тогда все три прямые PK, KA и KD образуют между собой углы по 90 градусов.
И тогда опять по определению угла между плоскостями угол между плоскостями (PAB)и (PCD) есть угол AKD, который (см. выше) . Значит угол между плоскостями (PAB) и (PCD) .

Т.к. AB = BC, то трапеция ABCD — равнобедренная, т.е. углы при основании равны, а так как их сумма , то они по . Но тогда Но тогда тоже имеет углы по и является равнобедренным и прямоугольным. Тогда его катеты в раз меньше гипотенузы BC и равно по .
Объем PKBC равен: