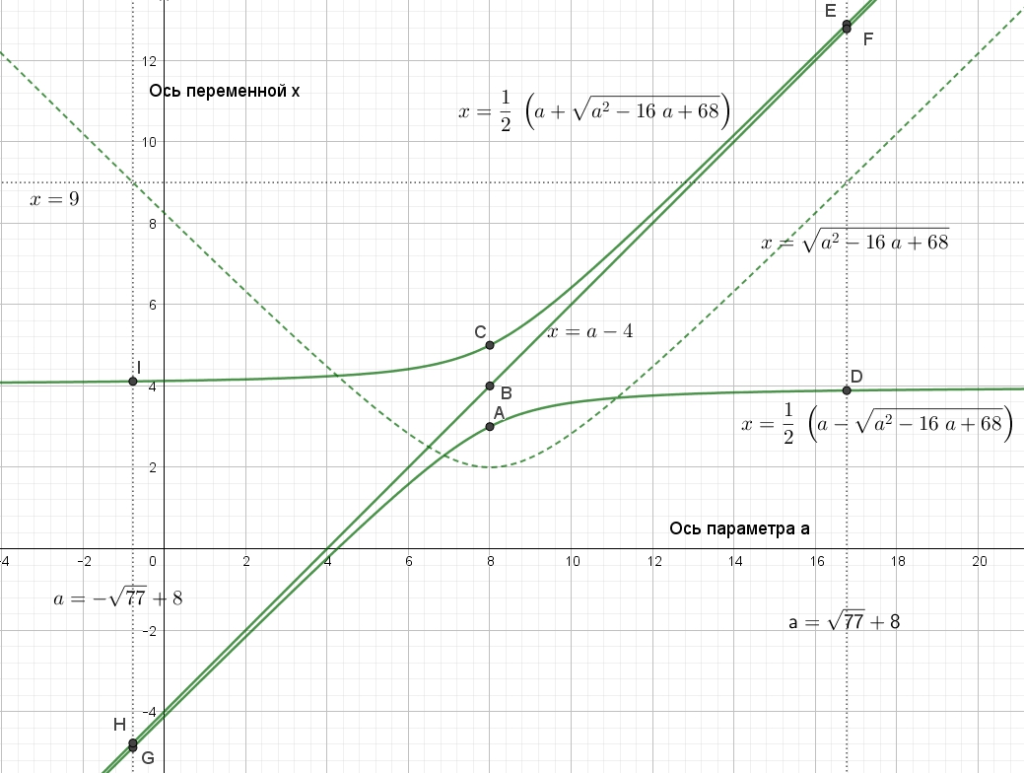
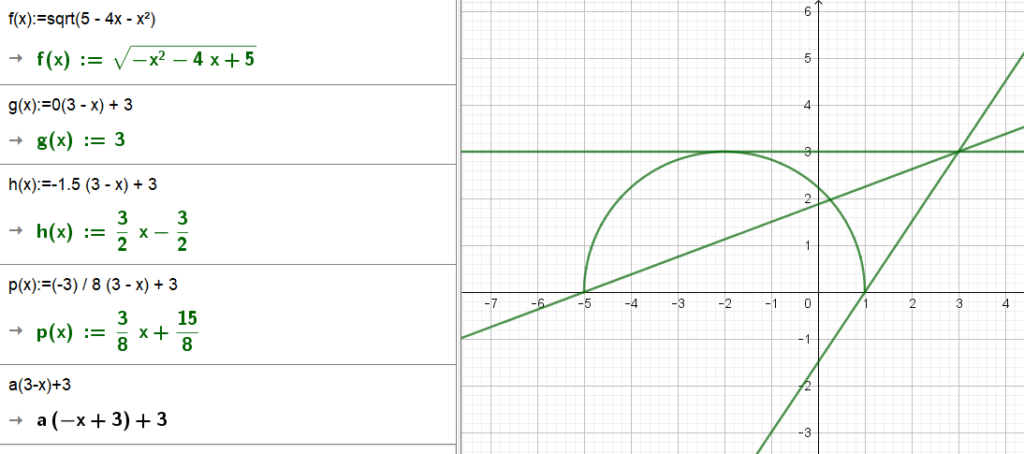
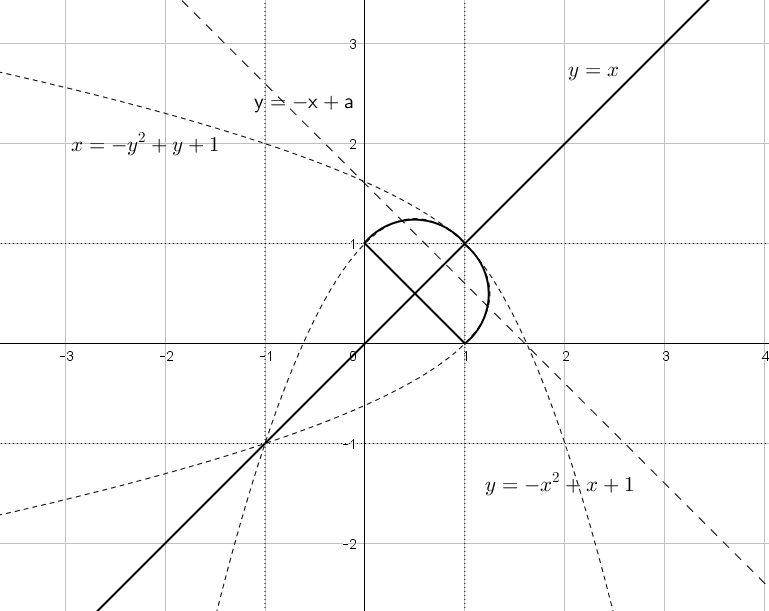
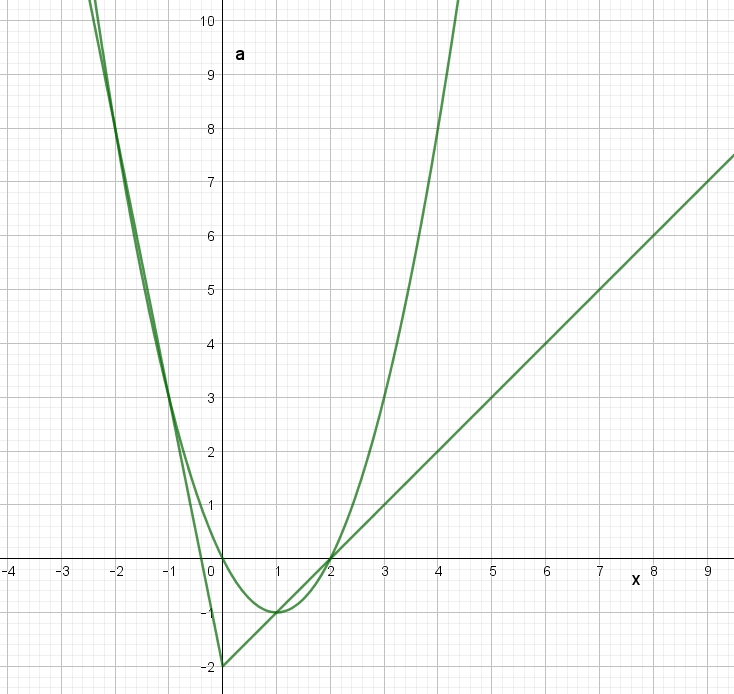
Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно четыре решения.
Рубрика: Задание 18 (параметры)
Реальный ЕГЭ 29 мая 2019, задание 18
Найти все значения , при каждом из которых уравнение имеет ровно два различных корня. Решим систему уравнений безотносительно к количеству корней : или Нарисуем на плоскости (a;x) оба множества Первым множеством является все точки Читать далее …
книга Высоцкого стр 23 задача 18
задача 18 стр 23 Высоцкого При каких множество решений неравенств и совпадают? Решим первое неравенство при . при или 4. при =0: при : — неверно, таких нет. при : верно при любом при — т.е. при — Читать далее …
Решение задания 18, вариант 36, Ященко 36 вариантов, ЕГЭ-2018
Делается по аналогии с вариантом 24
Решение задания 18, вариант 35, Ященко 36 вариантов, ЕГЭ-2018
Найдите все значения , при каждом из которых неравенство выполняется для всех значений . Перепишем Заметим, что слева — убывающая по функция, как бы ни раскрывались модули. Значит максимум у нее в левом конце отрезка . Читать далее …
Решение задания 18, вариант 34, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 33, Ященко 36 вариантов, ЕГЭ-2018
Найдите все значения , при каждом из которых неравенство выполняется для всех значений . Перепишем Заметим, что слева — убывающая по функция, как бы ни раскрывались модули. Значит максимум у нее в левом конце отрезка . Читать далее …
Решение задания 18, вариант 32, Ященко 36 вариантов, ЕГЭ-2018
Решение есть в самой книжке Лысенко на стр.250. Посмотрите там (нажмите на ссылку).
Решение задания 18, вариант 31, Ященко 36 вариантов, ЕГЭ-2018
Делается по аналогии с вариантом 23
Решение задания 18, вариант 30, Ященко 36 вариантов, ЕГЭ-2018
Найдите все значения , при каждом из которых уравнение имеет хотя бы одно решение на отрезке . Заметим, что на отрезке функция , т.е. точно . Заметим также, что отсюда сразу следует, что , т.к. если бы оно Читать далее …
Решение задания 18, вариант 29, Ященко 36 вариантов, ЕГЭ-2018
Найдите все значения , при каждом из которых уравнение имеет хотя бы один корень. Перепишем уравнение в виде Заметим, что слева стоит функция четных степеней, симметричная относительно оси , а справа — функция нечетных, симметричная относительно замены на . Как Читать далее …
Решение задания 18, вариант 28, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 27, Ященко 36 вариантов, ЕГЭ-2018
Решение есть в самой книжке Лысенко на стр.243. Посмотрите там (нажмите на ссылку).
Решение задания 18, вариант 26, Ященко 36 вариантов, ЕГЭ-2018
Делается по аналогии с вариантом 23
Решение задания 18, вариант 25, Ященко 36 вариантов, ЕГЭ-2018
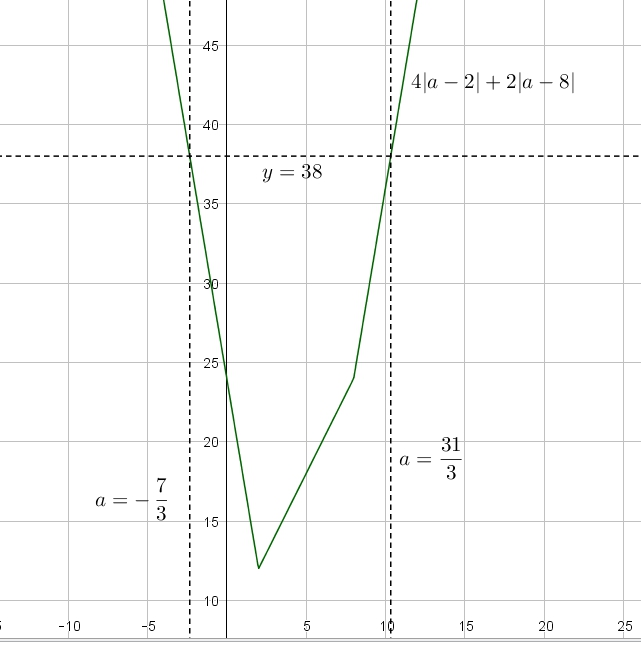
Найти все значения a, при каждом из которых неравенство выполняется для всех значений . Заметим, что слева — возрастающая по функция, как бы ни раскрывались модули. Значит, максимум у нее в правом конце отрезка . Значит, чтобы для Читать далее …
Решение задания 18, вариант 24, Ященко 36 вариантов, ЕГЭ-2018
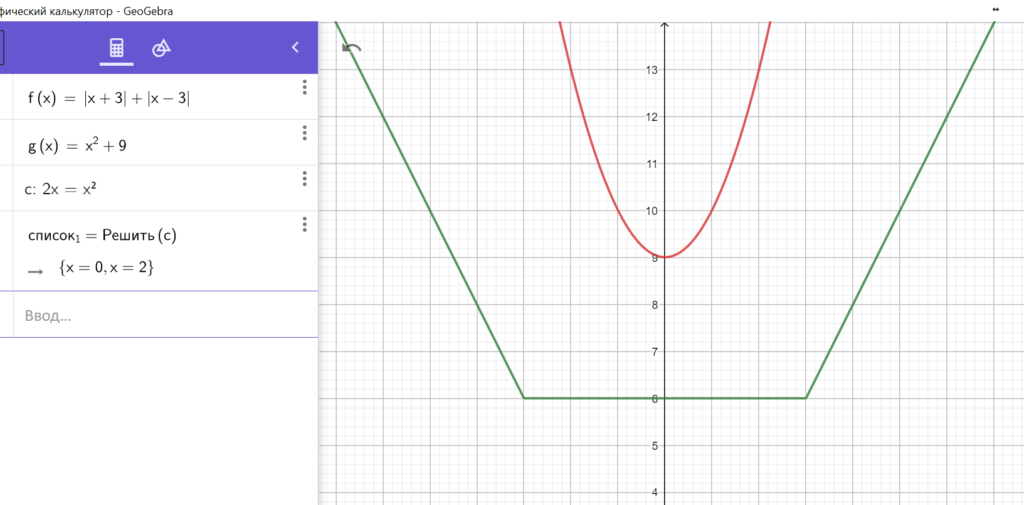
Найти все значения , при каждом из которых уравнение имеет единственный корень. Введем новый параметр и перепишем в виде или Заметим, что при изменении у нас слева парабола ездит вверх-вниз, а фигура тоже ездит вверх-вниз и при этом Читать далее …
Решение задания 18, вариант 23, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 22, Ященко 36 вариантов, ЕГЭ-2018
Решение есть в самой книжке Лысенко на стр.236. Посмотрите там (нажмите на ссылку).
Решение задания 18, вариант 21, Ященко 36 вариантов, ЕГЭ-2018
Решение аналогично варианту 17, который разобран в книжке Ященко в самой книжке Ященко на стр.230. Посмотрите там (нажмите на ссылку).
Решение задания 18, вариант 20, Ященко 36 вариантов, ЕГЭ-2018
Решение аналогично варианту 17, который разобран в книжке Ященко в самой книжке Ященко на стр.230. Посмотрите там (нажмите на ссылку).
Решение задания 18, вариант 19, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 18, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 17, Ященко 36 вариантов, ЕГЭ-2018
Решение есть в самой книжке Ященко на стр.230. Посмотрите там (нажмите на ссылку).
Решение задания 18, вариант 16, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 15, Ященко 36 вариантов, ЕГЭ-2018
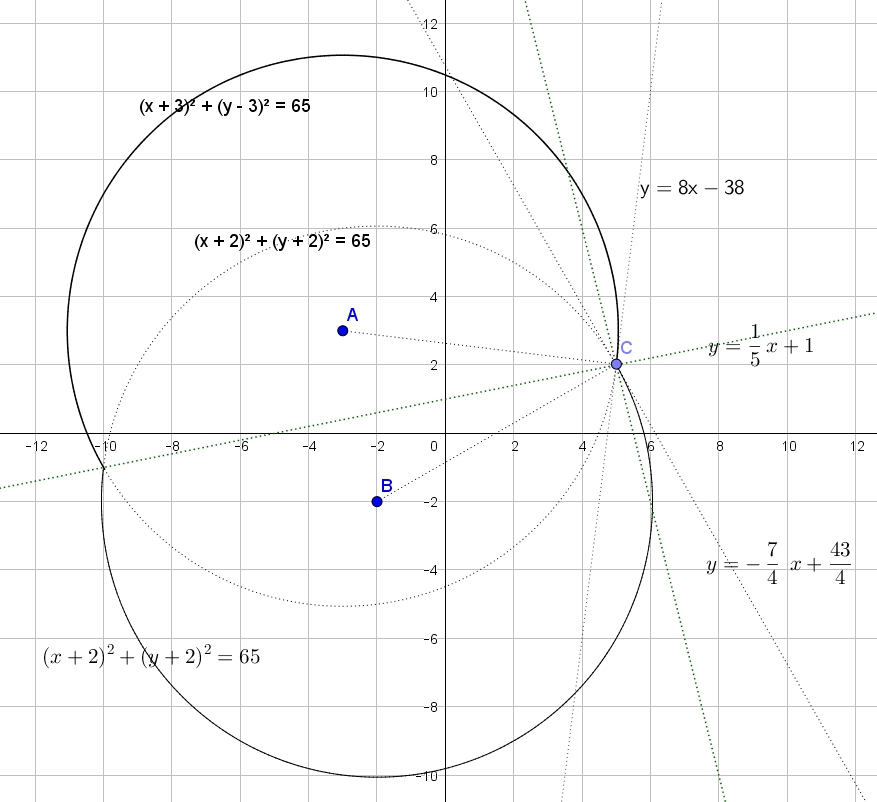
Найти все значения , при каждом из которых система уравнений имеет ровно два решения. Раскроем модуль: Ровно два решения будет, когда когда прямая в крайних положениях является касательной к окружностям — к Читать далее …
Решение задания 18, вариант 14, Ященко 36 вариантов, ЕГЭ-2018
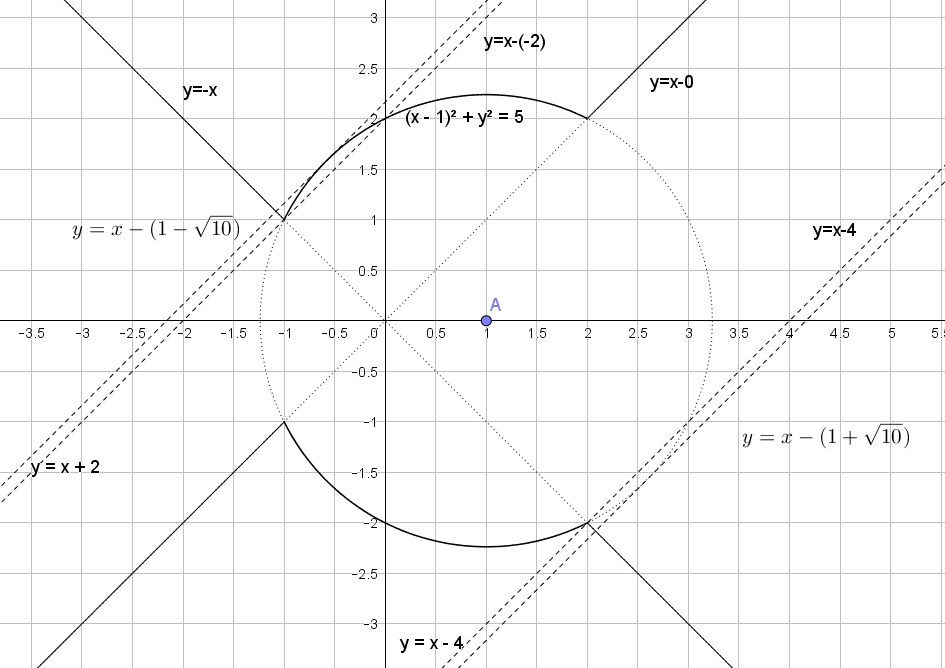
Найти все значения , при каждом из которых система имеет более двух решений. Раскроем модуль: Найдем при каких происходит касание прямой и окружности : Касание происходит, Читать далее …
Решение задания 18, вариант 13, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 18, вариант 12, Ященко 36 вариантов, ЕГЭ-2018
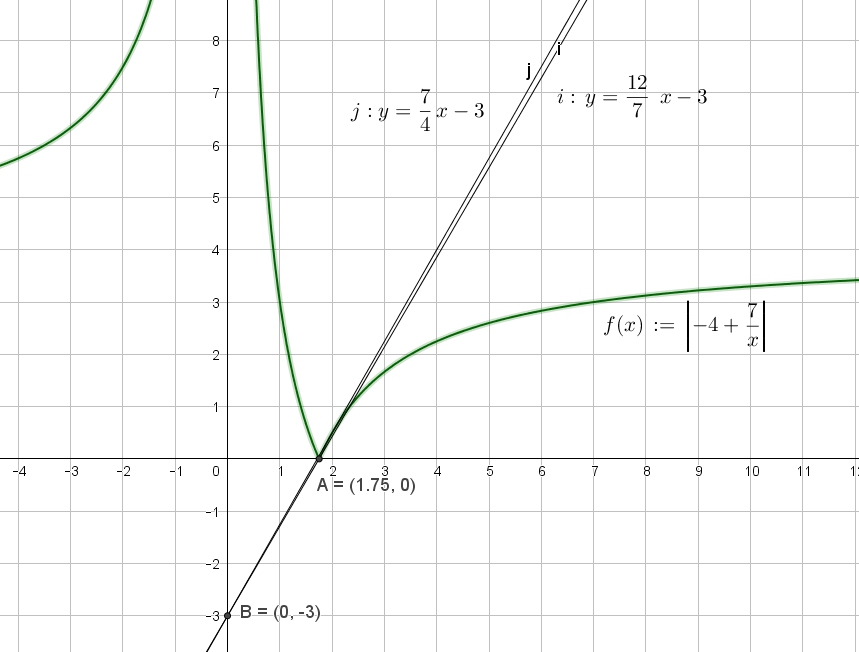
Найти все значения , при каждом из которых уравнение на промежутке имеет более двух корней. Решение также есть в самой книжке Лысенко на стр.222. Посмотрите там (нажмите на ссылку). Найдем координаты точки — где гипербола пересекает ось : , . Читать далее …
Решение задания 18, вариант 11, Ященко 36 вариантов, ЕГЭ-2018
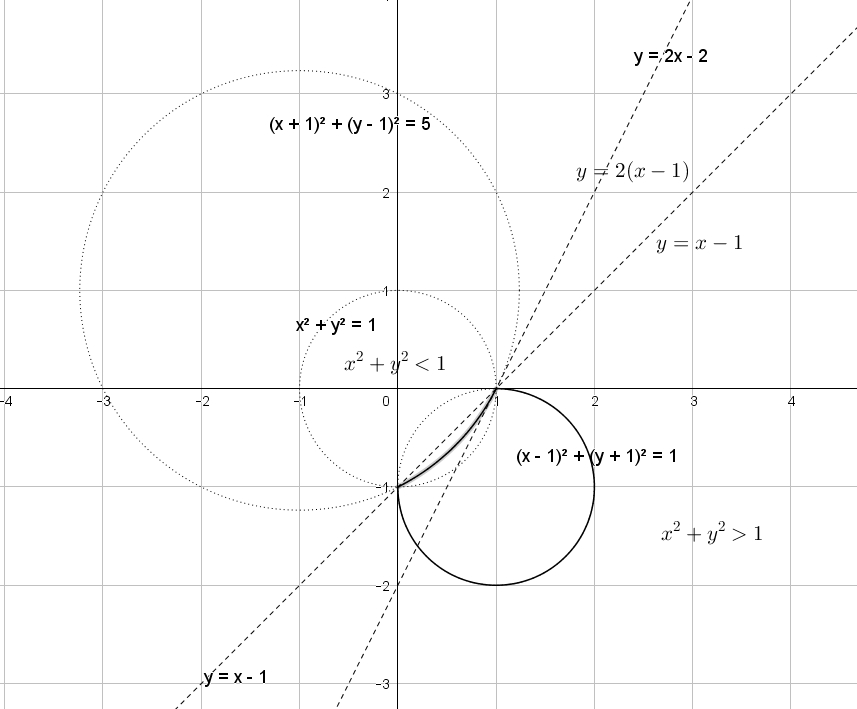
Найти все значения , при каждом из которых система уравнений имеет более двух решений. Раскроем модуль: Чтобы найти значение , при котором прямая касается левой верхней окружности , надо подставить прямую в окружность: Читать далее …
Решение задания 18, вариант 10, Ященко 36 вариантов, ЕГЭ-2018
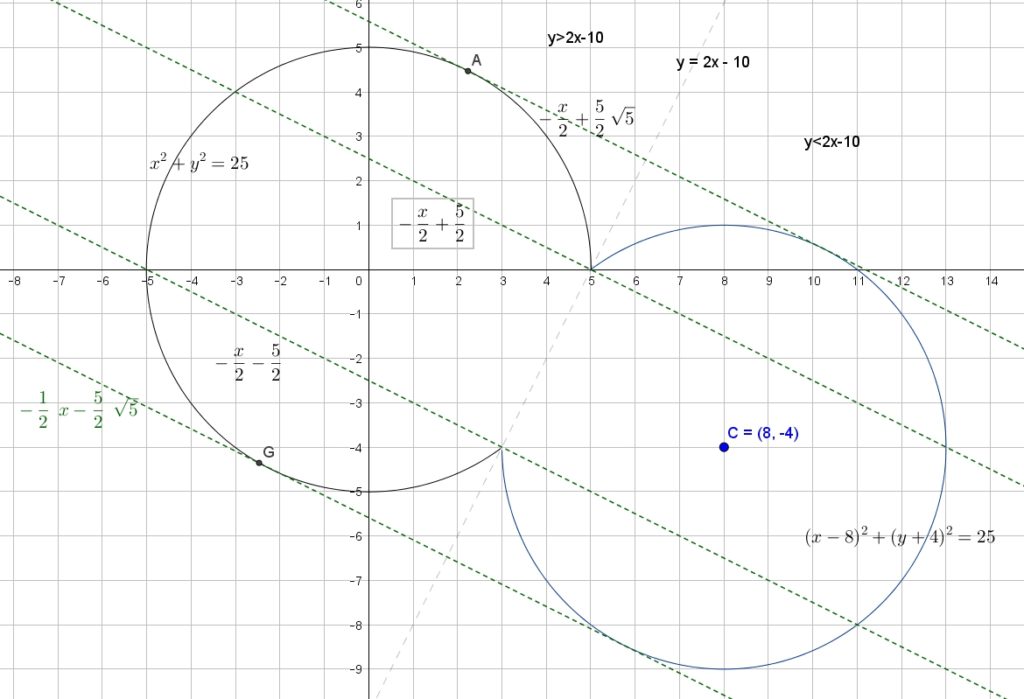
Найти все , при каждом из которых система уравнений имеет более двух решений. Раскроем модуль: Чтобы найти координаты точек касания и , заметим, что прямая должна проходить параллельно прямой и через центр Читать далее …
Решение задания 18, вариант 9, Ященко 36 вариантов, ЕГЭ-2018
Найти все значения a, при каждом из которых множество значений функции содержит отрезок Заметим, что, так как находится под корнем, то . При таких значениях знаменатель оказывается строго больше нуля всегда, при любом , а значит наша дробь Читать далее …
Решение задания 18, вариант 8, Ященко 36 вариантов, ЕГЭ-2018
Найти все значения a, при каждом из которых множество решений неравенства содержит отрезок Обозначим , тогда Заметим, что знаменатель при любом . Значит, мы можем домножить на знаменатель, т.к. нет таких , при которых знаменатель был бы равен Читать далее …
Решение задания 18, вариант 7, Ященко 36 вариантов, ЕГЭ-2018
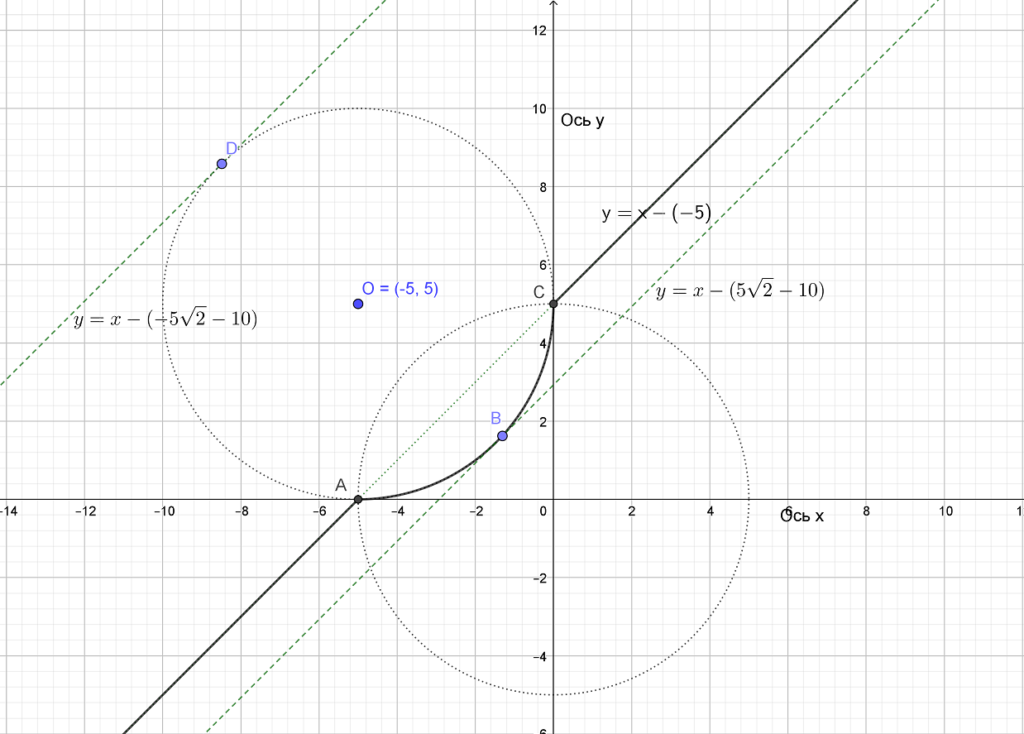
Найти все значения a, при каждом из которых система уравнений имеет более одного решения. Раскроем модуль: Найдем значение параметра при котором прямая касается окружности с центром O(-5,5), для этого подставим вместо в Читать далее …
Решение задания 18, вариант 6, Ященко 36 вариантов, ЕГЭ-2018
Решается аналогично решению варианта 4, посмотрите решение в варианте 4
Решение задания 18, вариант 5, Ященко 36 вариантов, ЕГЭ-2018
Решается аналогично решению варианта 4, посмотрите решение в варианте 4
Решение задания 18, вариант 4, Ященко 36 вариантов, ЕГЭ-2018
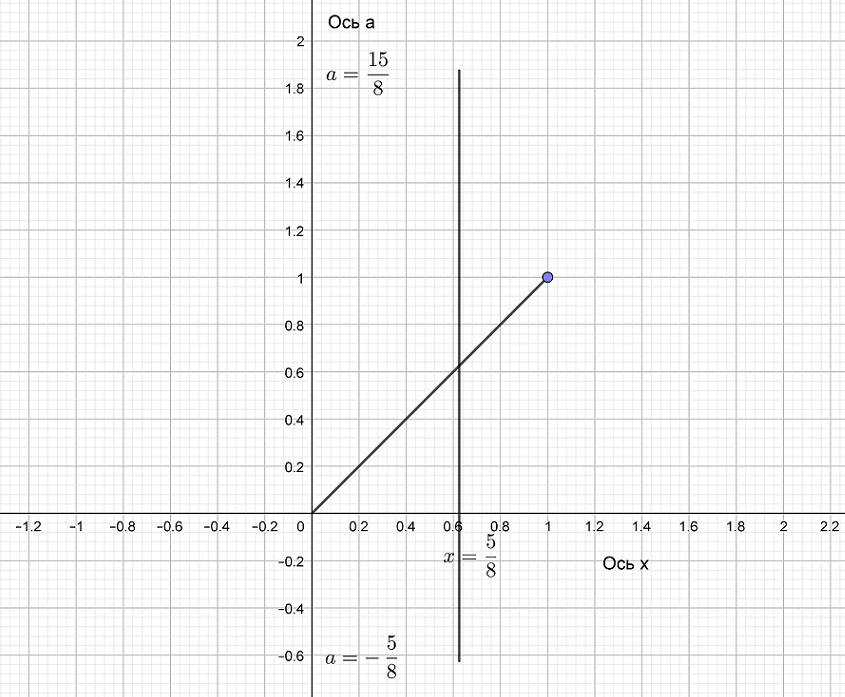
Найти все значения a, при каждом из которых уравнение имеет ровно один корень на отрезке . Напишем ОДЗ: Вынесем за скобку: Получаем первый корень , подставляем его в ОДЗ и получаем ограничения Читать далее …
Решение задания 18, вариант 3, Ященко 36 вариантов, ЕГЭ-2018
Решается аналогично решению варианта 1, посмотрите решение в варианте 1
Решение задания 18, вариант 2, Ященко 36 вариантов, ЕГЭ-2018
Решается аналогично решению варианта 1, посмотрите решение в варианте 1
Решение задания 18, вариант 1, Ященко 36 вариантов, ЕГЭ-2018
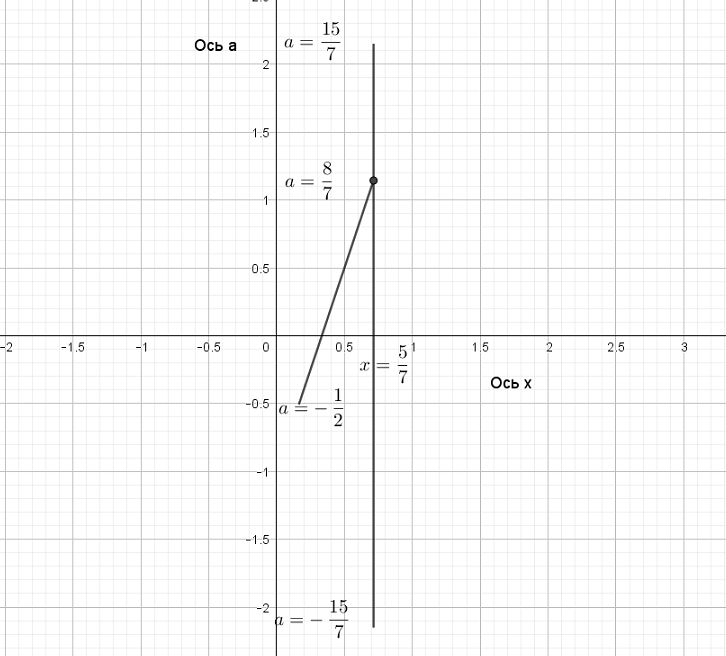
Найти все значения , при каждом из которых уравнение имеет ровно один корень. Напишем ОДЗ: Наше ОДЗ — это треугольник между точками : При этом отрезок BC входит в ОДЗ, точки B и С Читать далее …