Решение задания 18, вариант 1, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике

Найти все значения $a$ , при каждом из которых уравнение

$\sqrt{5-7x} \cdot \ln(9x^2-a^2) = \sqrt{5-7x} \cdot \ln(3x+a)$

имеет ровно один корень.

Напишем ОДЗ:

$\begin{Bmatrix}{5-7x \ge 0}\\{3x+a > 0}\\{9x^2-a^2 =(3x-a)(3x+a)>0}\end{matrix}$

$\begin{Bmatrix}{x \le \frac57}\\{a > -3x}\\{a<3x}\end{matrix}$

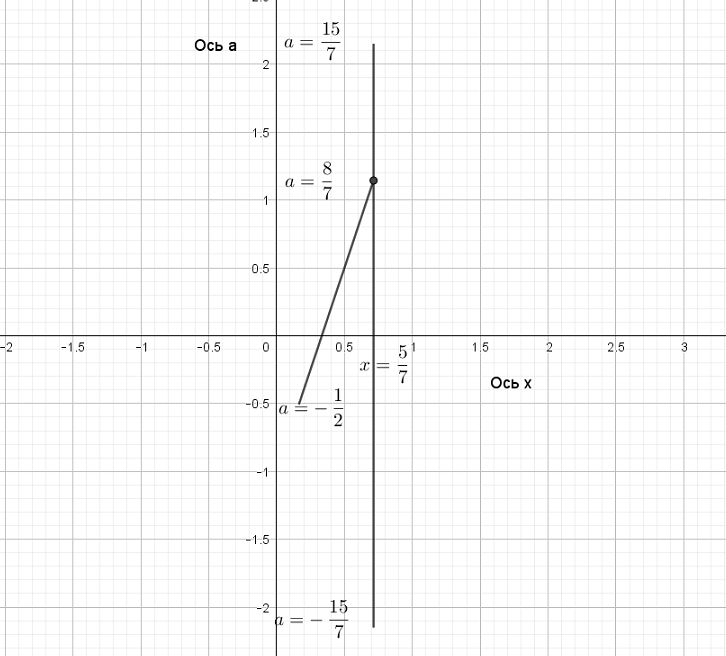
Наше ОДЗ — это треугольник между точками $A(0;0),B(x=\frac57;a=\frac{15}{7}),C(x=\frac57;a=-\frac{15}{7})$ :

При этом отрезок BC входит в ОДЗ, точки B и С — входят, а отрезки AB и AC — не входят, точка A — не входит в ОДЗ.

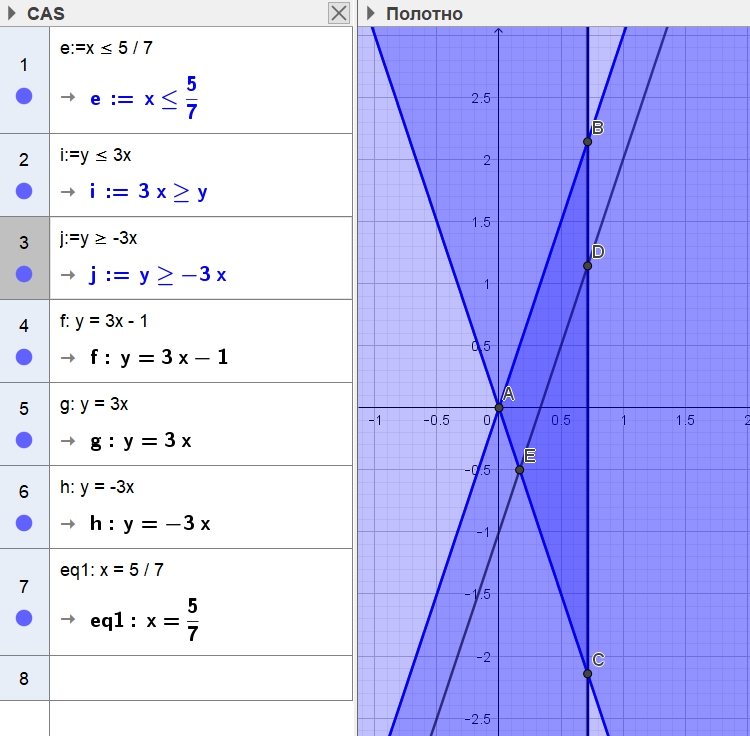
Ниже график функции $z=9x^2-a^2$ . Это для лучшего понимания в каких квадрантах (областях) плоскости $(x;a)$ верно неравенство $9x^2-a^2>0$ из ОДЗ, т.е. в каких точках плоскости $(x;a)$ выражение $9x^2-a^2$ положительно ( $9x^2-a^2>0$ ) и в каких точках отрицательно ( $9x^2-a^2<0$ ):

Чтобы еще раз прокрутить изображение, откройте картинку в новой вкладке и обновите ее несколько раз по F5 🙂

Преобразуем:

$\sqrt{5-7x} \cdot \{ \ln(9x^2-a^2) - \ln(3x+a) \} =0$

$\sqrt{5-7x} \cdot \{ \ln[(3x-a)(3x+a)] - \ln(3x+a) \} =0$

$\sqrt{5-7x} \cdot \ln(3x-a) =0$

Сразу виден первый корень $x_1=\frac57$ , подставляя его в ОДЗ, получаем:

$\begin{Bmatrix} {x_1=\frac57}\\ {a > -\frac{15}{7}}\\{a<\frac{15}{7}}\end{matrix}$

Т.е. при $-\frac{15}{7}<a<\frac{15}{7}$ есть первый корень $x_1=\frac57$ . Это отрезок BC.

Второй корень найдем из условия $\ln(3x-a) =0$ , т.е. $3x-a =1$ , $a=3x-1$ или $x_2=\frac{a+1}{3}$ Подставляя этот корень $x_2=\frac{a+1}{3}$ в ОДЗ, получаем:

$\begin{Bmatrix}{ \frac{a+1}{3} \le \frac57}\\{a > -3\cdot\frac{a+1}{3}}\\{a<3\cdot\frac{a+1}{3}}\end{matrix}$

$\begin{Bmatrix}{ a \le \frac{15}{7}-1=\frac{8}{7}}\\{a > -a-1}\\{a<a+1}\end{matrix}$

$\begin{Bmatrix}{ a \le \frac{8}{7}}\\{a > -\frac12}\\{0<1}\end{matrix}$

Итак, при $-\frac12<a\le \frac{8}{7}$ есть второй корень $x_2=\frac{a+1}{3}$
Это отрезок DE.

Вспомним, что при $-\frac{15}{7}<a<\frac{15}{7}$ есть первый корень $x_1=\frac57$
Т.е. при $-\frac12<a\le \frac{8}{7}$ есть в итоге два корня одновременно: $x_1=\frac57$ и $x_2=\frac{a+1}{3}$
Казалось бы, вот ответ:
Ровно один корень (и равный $\frac{a+1}{3}$ ) есть при $-\frac{15}{7}<a\le -\frac12$ и при $\frac{8}{7}<a< \frac{15}{7}$
Но! Проверим где эти корни совпадают: $x_1=\frac57=x_2=\frac{a+1}{3} \Rightarrow a= \frac87$ нужно включить в ответ.

Ответ: ровно один корень есть при $-\frac{15}{7}<a\le -\frac12$ и при $\frac{8}{7}\le a< \frac{15}{7}$

Плюс также вы можете посмотреть решение в самой книжке Ященко на стр.207. Нажмите на ссылку.

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru

Один комментарий к “Решение задания 18, вариант 1, Ященко 36 вариантов, ЕГЭ-2018”