Окружность с центром O1 касается оснований BC и AD, а также боковой стороны AB трапеции ABCD. Окружность с центром O2 касается сторон BC, CD и AD. Известно, что AB=9, BC=8, CD=4, AD=15. а) Докажите, что прямая 0102 параллельна основаниям трапеции Читать далее …
Рубрика: Задание 16 (планиметрия)
Реальный ЕГЭ 2го июня 2017, задание 16
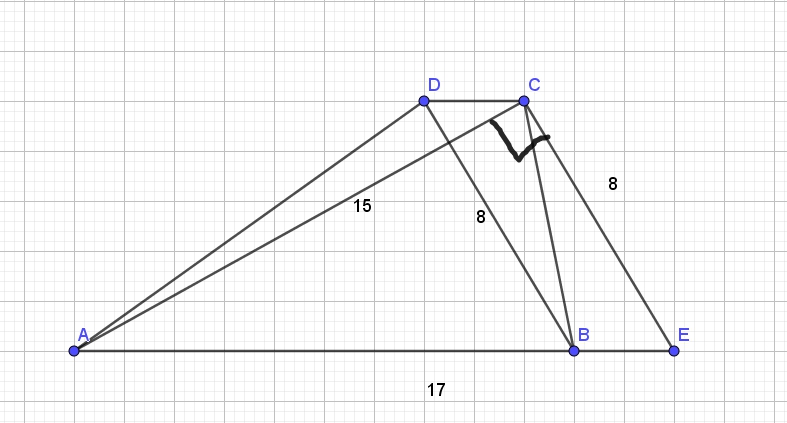
Дана трапеция ABCD с диагоналями равными 8 и 15. Сумма оснований трапеции равна 17. а) Докажите, что диагонали перпендикулярны. б) Найдите высоту трапеции Сделаем дополнительное построение — проведем . Тогда , а т.к. BECD — параллелограмм. В треугольнике ACE стороны Читать далее …
Реальный ЕГЭ 29 мая 2019, задание 16
В остроугольном треугольнике ABC все стороны различны. Прямая, содержащая высоту BH треугольника ABC, вторично пересекает описанную около этого треугольника окружность в точке K. Отрезок BN — диаметр этой окружности. a) Докажите, что AN=CK b) Найдите NK, если радиус описанной около Читать далее …
Решение задания 16, вариант 36, Ященко 36 вариантов, ЕГЭ-2018
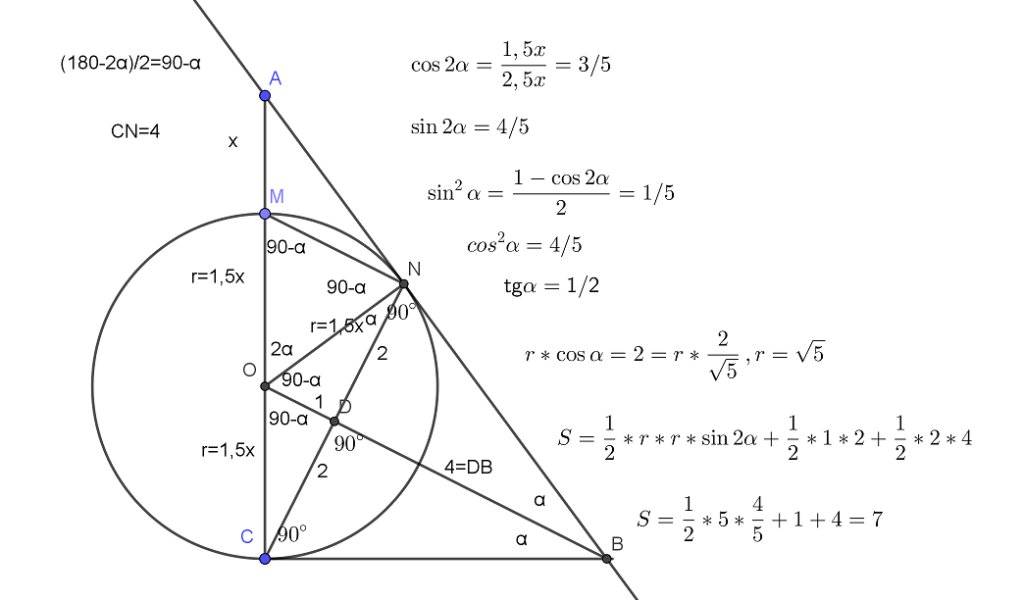
Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка М. Окружность с центром О и диаметром СМ касается гипотенузы в точке N. а) Докажите, что MN и ВО параллельны. б) Найдите площадь четырёхугольника BOMN,если СN=4 и Читать далее …
Решение задания 16, вариант 35, Ященко 36 вариантов, ЕГЭ-2018
Отрезок, соединяющий середины M и N оснований BC и AD соответственно трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность. а) Докажите, что трапеция ABCD равнобедренная. б) Известно, что радиус этих окружностей равен 4, а Читать далее …
Решение задания 16, вариант 34, Ященко 36 вариантов, ЕГЭ-2018
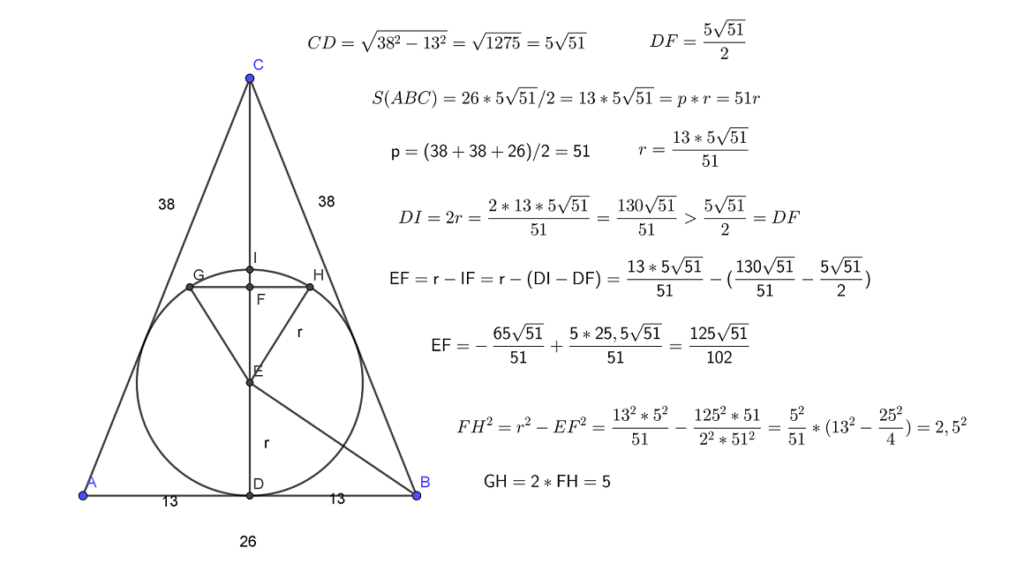
Основание и боковая сторона равнобедренного треугольника равны 10 и 12 соответственно. а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник. б) Найдите длину отрезка этой средней линии, заключенного внутри окружности. Решение полностью аналогично варианту 15, посмотрите Читать далее …
Решение задания 16, вариант 33, Ященко 36 вариантов, ЕГЭ-2018
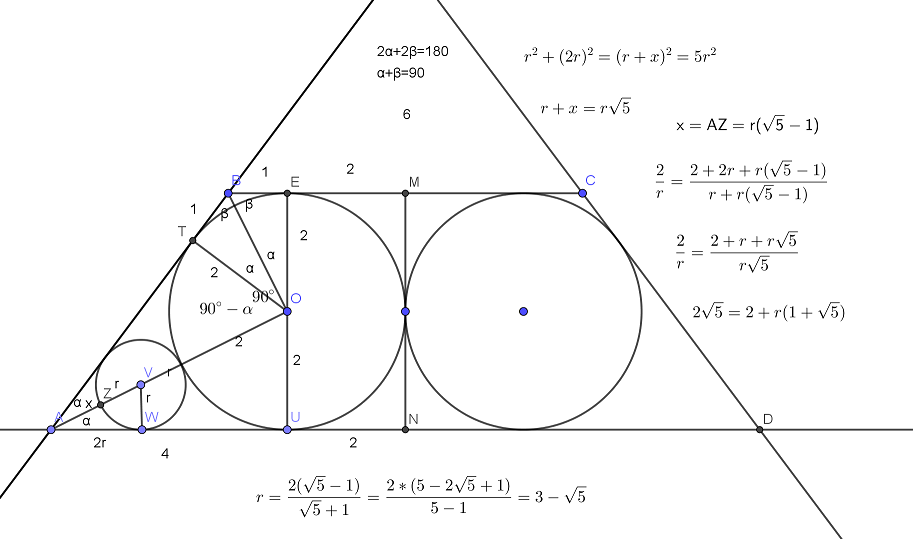
Отрезок, соединяющий середины M и N оснований BC и AD соответственно трапеции ABCD, разбивает её на две трапеции, в каждую из которых можно вписать окружность. а) Докажите, что трапеция ABCD равнобедренная. б) Известно, что радиус этих окружностей равен 2, а Читать далее …
Решение задания 16, вариант 32, Ященко 36 вариантов, ЕГЭ-2018
Вневписанная окружность равнобедренного треугольника касается его боковой стороны. а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание. б) Известно, что радиус этой окружности в 6 раз больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной Читать далее …
Решение задания 16, вариант 31, Ященко 36 вариантов, ЕГЭ-2018
Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее …
Решение задания 16, вариант 30, Ященко 36 вариантов, ЕГЭ-2018
Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее …
Решение задания 16, вариант 29, Ященко 36 вариантов, ЕГЭ-2018
Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее …
Решение задания 16, вариант 28, Ященко 36 вариантов, ЕГЭ-2018
Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее …
Решение задания 16, вариант 27, Ященко 36 вариантов, ЕГЭ-2018
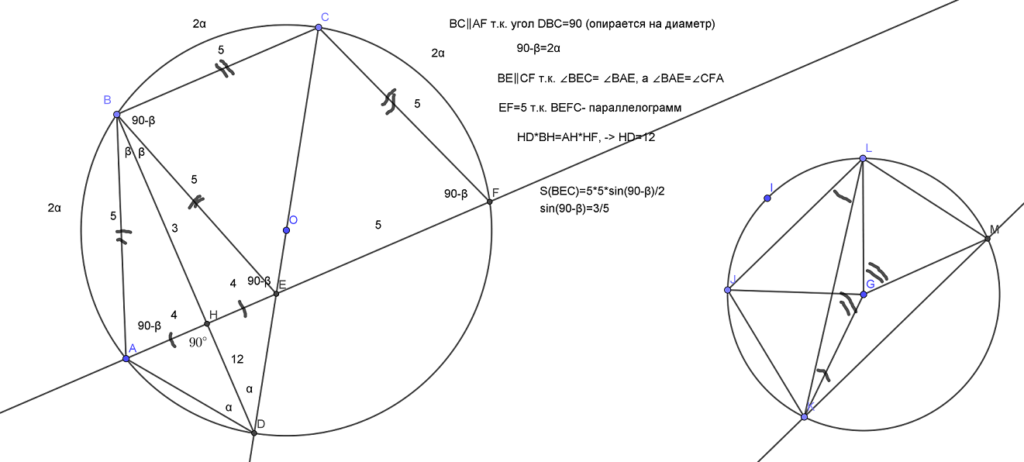
Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра AH к диагонали BD пересекает сторону CD в точке E, а окружность — в точке F, причём H — середина AE. а) Докажите, что четырёхугольник BCFE Читать далее …
Решение задания 16, вариант 26, Ященко 36 вариантов, ЕГЭ-2018
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°. а) Докажите, что ∠CBE = ∠COE. б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, Читать далее …
Решение задания 16, вариант 25, Ященко 36 вариантов, ЕГЭ-2018
Основание и боковая сторона равнобедренного треугольника равны 26 и 31 соответственно. а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник. б) Найдите длину отрезка этой средней линии, заключенного внутри окружности. Решение аналогично варианту 15, посмотрите решение Читать далее …
Решение задания 16, вариант 24, Ященко 36 вариантов, ЕГЭ-2018
В треугольнике ABC известно, что ∠BAC=60°, ∠ABC=45°. Продолжения высот треугольника ABC пересекают описанную около него окружность в точках M,N,P. а) Докажите, что треугольник MNP — прямоугольный. б) Найдите площадь треугольника MNP, если известно, что BC = 10. Решается в точности Читать далее …
Решение задания 16, вариант 23, Ященко 36 вариантов, ЕГЭ-2018
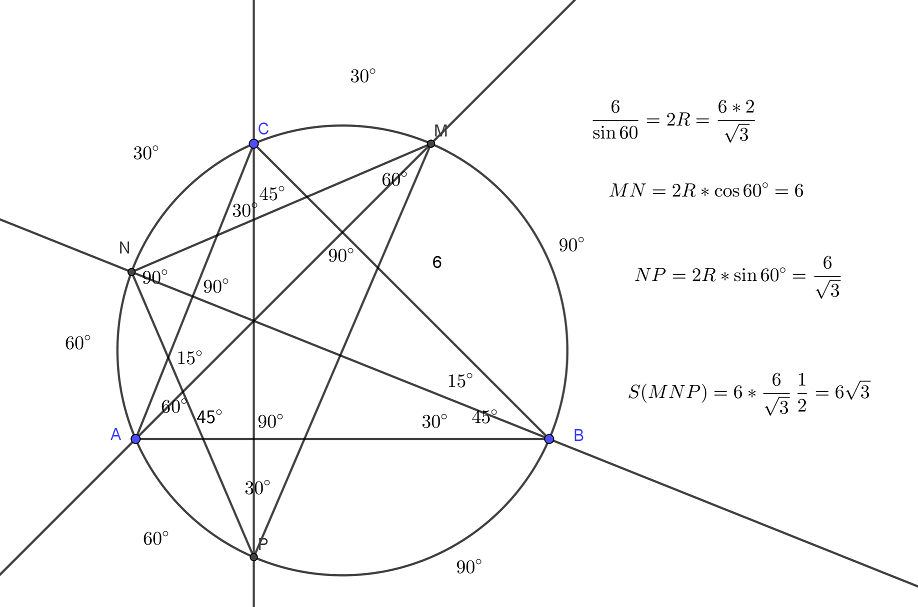
В треугольнике ABC известно, что ∠BAC=60°, ∠ABC=45°. Продолжения высот треугольника ABC пересекают описанную около него окружность в точках M,N,P. а) Докажите, что треугольник MNP — прямоугольный. б) Найдите площадь треугольника MNP, если известно, что BC = 6. Решение смотри на Читать далее …
Решение задания 16, вариант 22, Ященко 36 вариантов, ЕГЭ-2018
Основание и боковая сторона равнобедренного треугольника равны 34 и 49 соответственно. а) Докажите, что средняя линия треугольника, параллельная основанию, пересекает окружность, вписанную в треугольник. б) Найдите длину отрезка этой средней линии, заключенного внутри окружности. Решается в точности как вариант 15, Читать далее …
Решение задания 16, вариант 21, Ященко 36 вариантов, ЕГЭ-2018
Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее …
Решение задания 16, вариант 20, Ященко 36 вариантов, ЕГЭ-2018
Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее …
Решение задания 16, вариант 19, Ященко 36 вариантов, ЕГЭ-2018
Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее …
Решение задания 16, вариант 18, Ященко 36 вариантов, ЕГЭ-2018
Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее …
Решение задания 16, вариант 17, Ященко 36 вариантов, ЕГЭ-2018
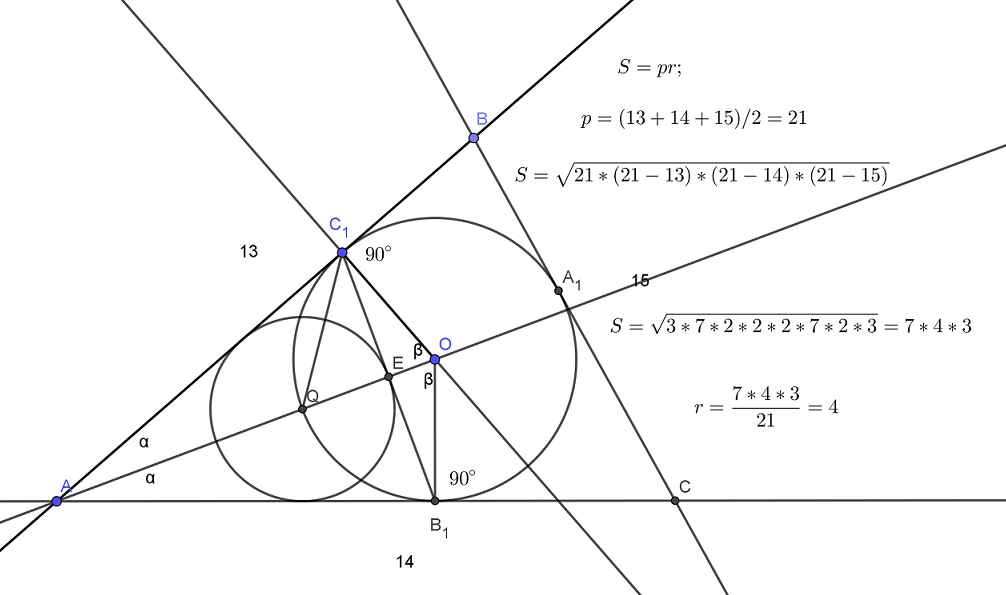
Окружность с центром O, вписанная в треугольник ABC, касается его сторон АВ, АС и ВС в точках , и соответственно. Биссектриса угла А пересекает эту окружность в точке Q, лежащей внутри треугольника . а) Докажите, что – биссектриса угла . Читать далее …
Решение задания 16, вариант 16, Ященко 36 вариантов, ЕГЭ-2018
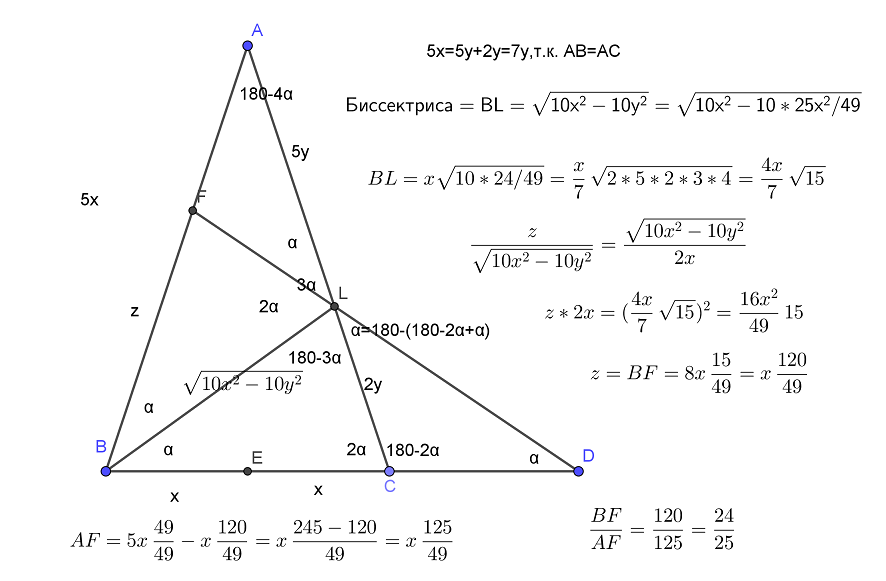
На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD. а) Докажите, что треугольник DCL равнобедренный. б) Известно, что . В каком отношении прямая DL делит сторону Читать далее …
Решение задания 16, вариант 15, Ященко 36 вариантов, ЕГЭ-2018
Решение задания 16, вариант 14, Ященко 36 вариантов, ЕГЭ-2018
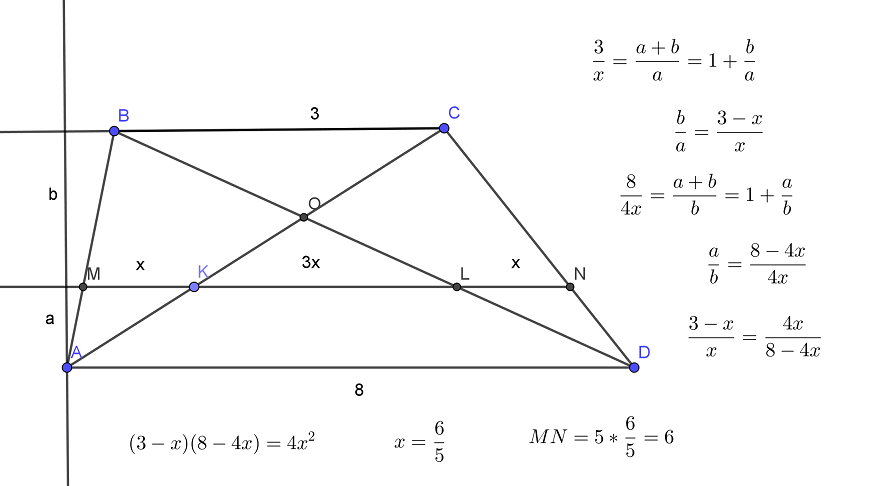
Прямая, параллельная основаниям BC и AD трапеции ABCD, пересекает боковые стороны AB и CD в точках M и N соответственно. Диагонали AC и BD пересекаются в точке O. Прямая MN пересекает стороны OA и OD треугольника AOD в точках K Читать далее …
Решение задания 16, вариант 13, Ященко 36 вариантов, ЕГЭ-2018

Вневписанная окружность равнобедренного треугольника касается его боковой стороны а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание. б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной Читать далее …
Решение задания 16, вариант 12, Ященко 36 вариантов, ЕГЭ-2018
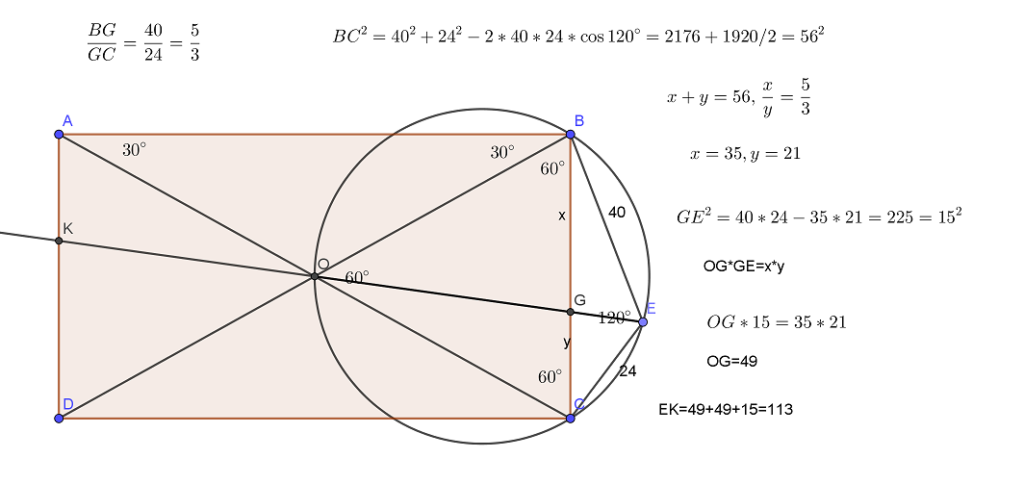
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°. а) Докажите, что ∠CBE = ∠COE. б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, Читать далее …
Решение задания 16, вариант 11, Ященко 36 вариантов, ЕГЭ-2018
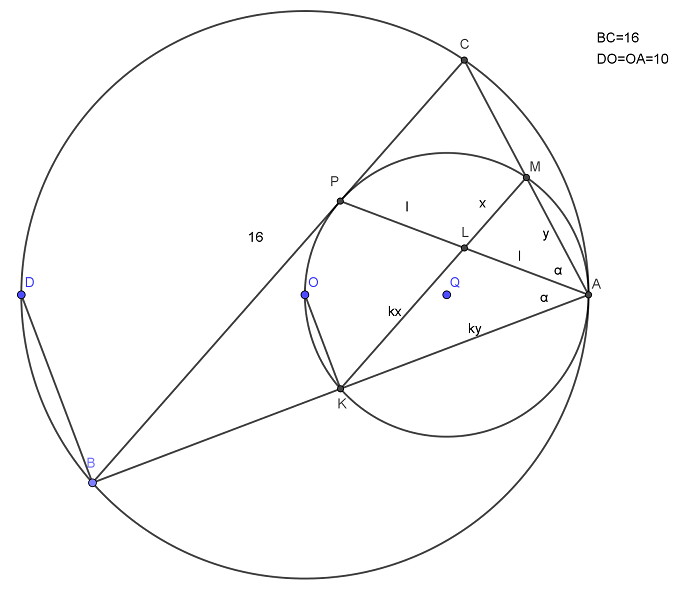
Две окружности касаются внутренним образом в точке A, причем меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно. a) Докажите, что прямые Читать далее …
Решение задания 16, вариант 10, Ященко 36 вариантов, ЕГЭ-2018
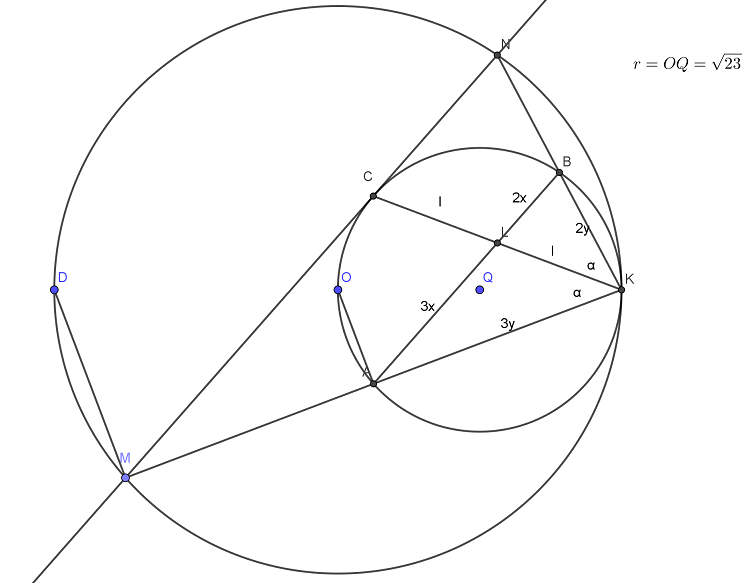
Две окружности касаются внутренним образом в точке K, причем меньшая проходит через центр большей. Хорда МN большей окружности касается меньшей в точке С.Хорды КМ и КN пересекают меньшую окружность в точках А и В соответственно,а отрезки КС и АВ пересекаются Читать далее …
Решение задания 16, вариант 9, Ященко 36 вариантов, ЕГЭ-2018
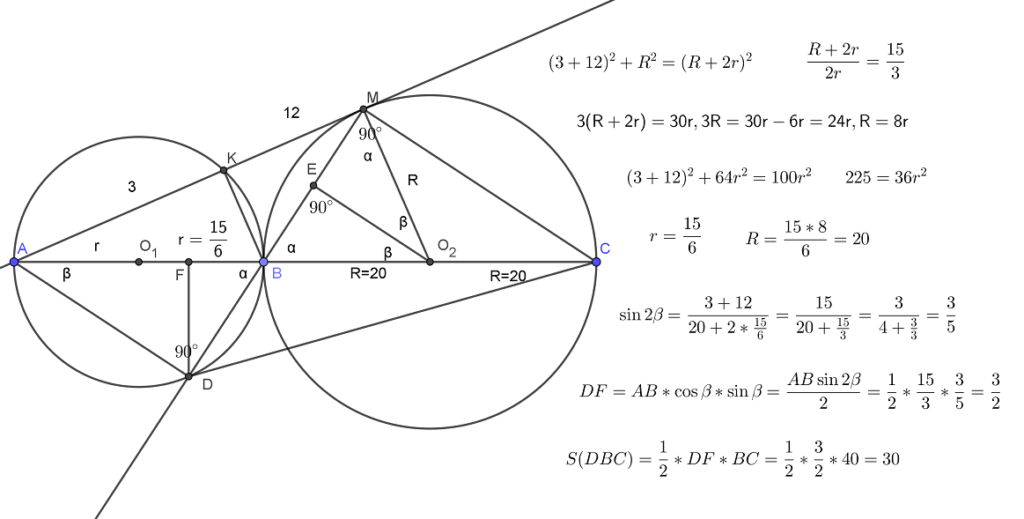
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке Читать далее …
Решение задания 16, вариант 8, Ященко 36 вариантов, ЕГЭ-2018
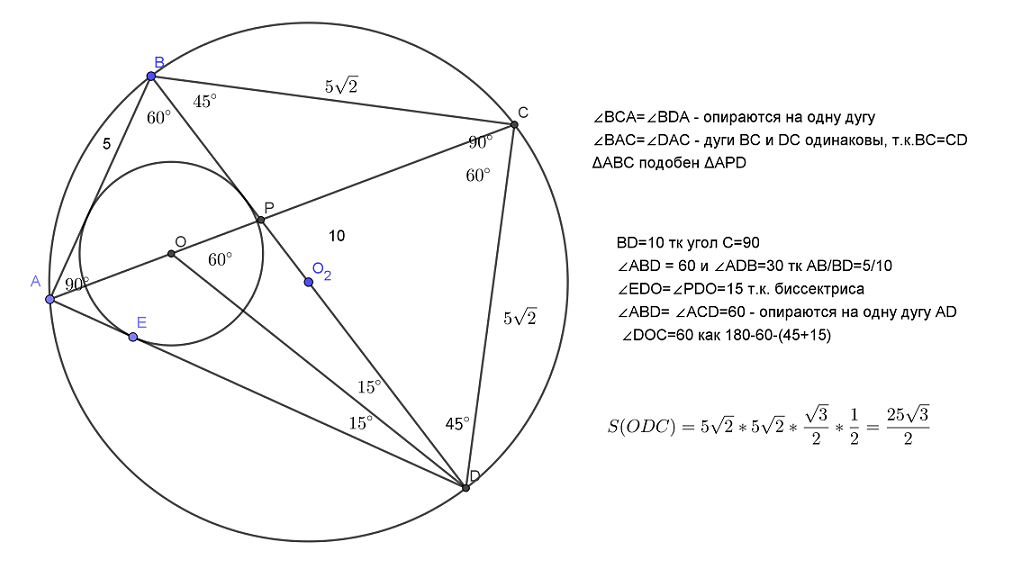
Диагонали AC и BD четырехугольника ABCD, вписанного в окружность, пересекаются в т. P, причем BC=CD. a) Докажите, что AB:BC=AP:PD b) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр Читать далее …
Решение задания 16, вариант 7, Ященко 36 вариантов, ЕГЭ-2018
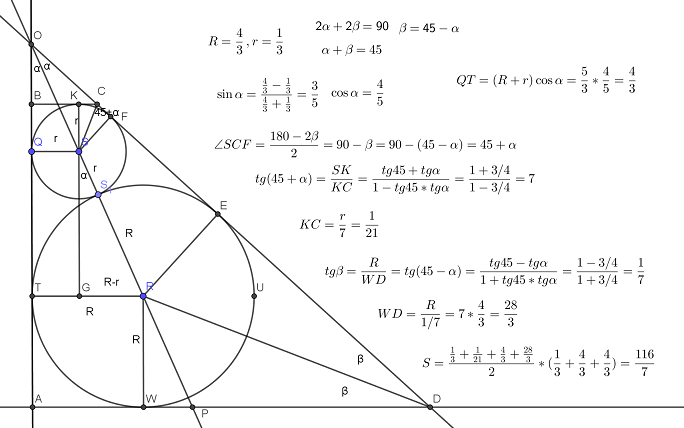
В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая — боковых сторон, меньшего основания BC и первой окружности. a) Прямая, проходящая через центры окружностей, пересекает Читать далее …
Решение задания 16, вариант 6, Ященко 36 вариантов, ЕГЭ-2018
В равнобедренной трапеции ABCD основание AD в три раза больше основания BC. a) Докажите, что высота BH трапеции разбивает основание AD на отрезки, один из которых в два раза больше другого b) Найдите расстояние от вершины B до середины диагонали Читать далее …
Решение задания 16, вариант 5, Ященко 36 вариантов, ЕГЭ-2018
В равнобедренной трапеции ABCD основание AD в три раза больше основания BC. a) Докажите, что высота BH трапеции разбивает основание AD на отрезки, один из которых в два раза больше другого b) Найдите расстояние от вершины B до середины диагонали Читать далее …
Решение задания 16, вариант 4, Ященко 36 вариантов, ЕГЭ-2018
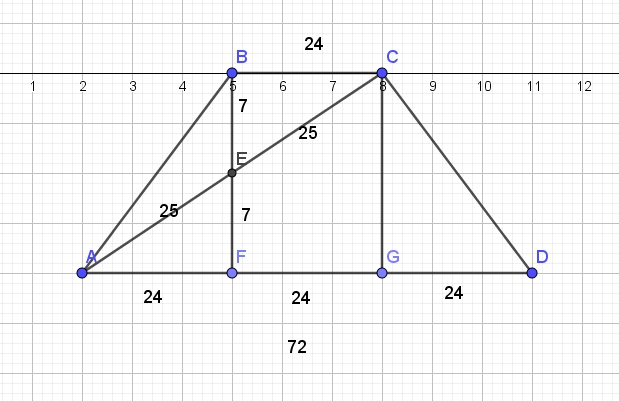
В равнобедренной трапеции ABCD основание AD в три раза больше основания BC. a) Докажите, что высота BF трапеции разбивает основание AD на отрезки, один из которых в два раза больше другого b) Найдите расстояние от вершины B до середины диагонали Читать далее …
Решение задания 16, вариант 3, Ященко 36 вариантов, ЕГЭ-2018
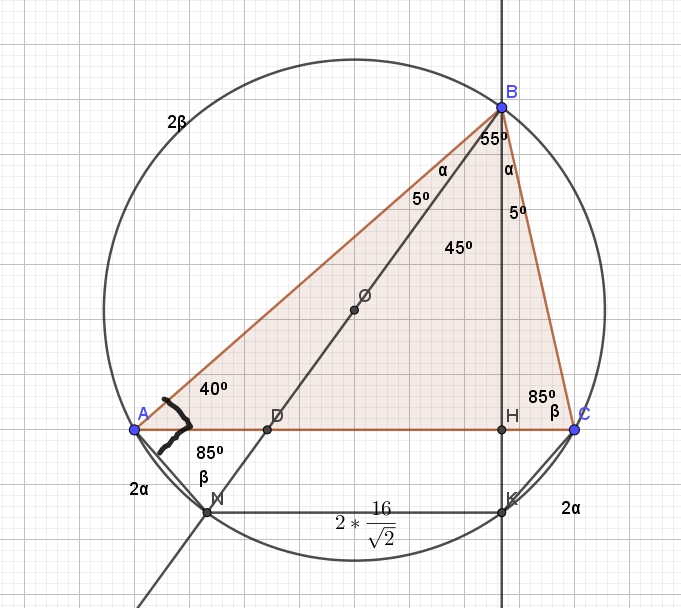
В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM — прямые. a) Докажите, что BM=CM b) Найдите угол ABC, если угол BCD=85 градусов, а расстояние от точки Читать далее …
Решение задания 16, вариант 2, Ященко 36 вариантов, ЕГЭ-2018
В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM — прямые. a) Докажите, что BM=CM b) Найдите угол ABC, если угол BCD=57 градусов, а расстояние от точки Читать далее …
Решение задания 16, вариант 1, Ященко 36 вариантов, ЕГЭ-2018
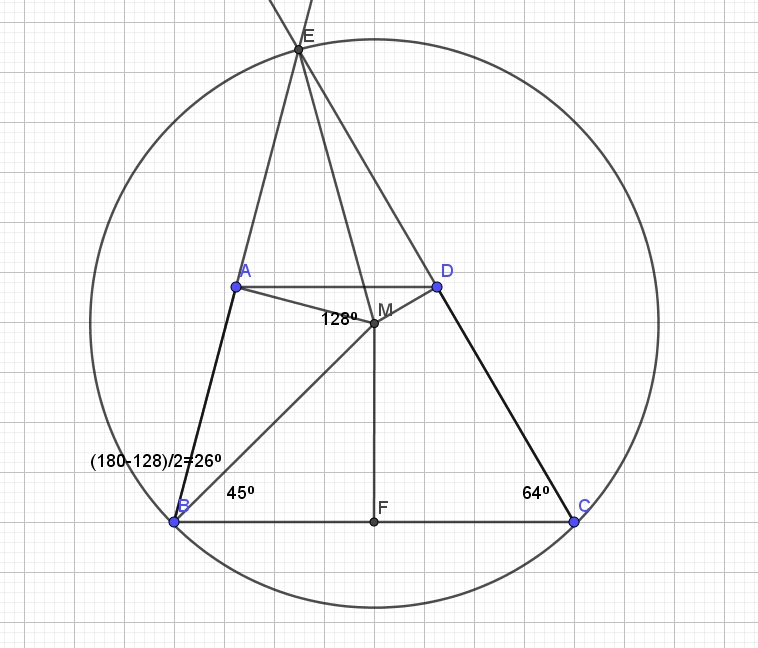
В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM — прямые. a) Докажите, что BM=CM b) Найдите угол ABC, если угол BCD=64 градуса, а расстояние от точки Читать далее …
Решение задания 16, вариант 10, Ященко 36 вариантов, ЕГЭ-2017
Основные идеи: Точки A и B — середины KM и KN соответственно, т.к. внутренняя окружность проходит через центр внешней и т.к. по двум углам (). как средняя линия. Т.к. , то дуги BC и AC равны (т.к. , то , Читать далее …