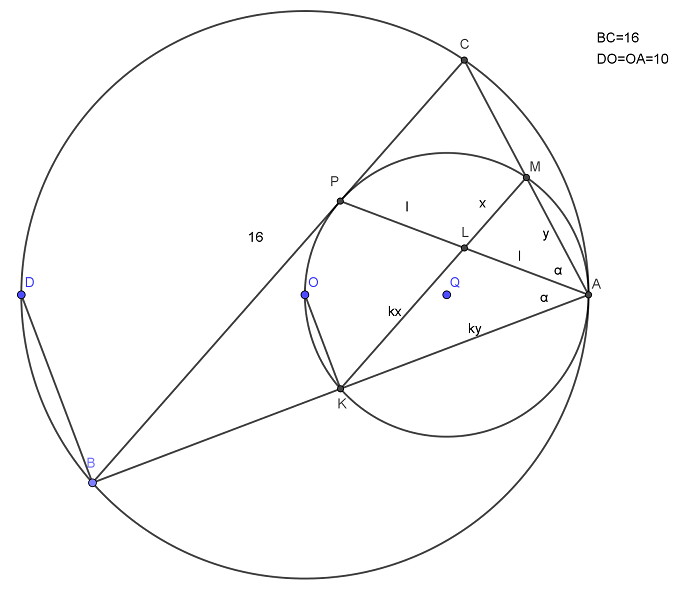
Решение задания 16, вариант 11, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике

Две окружности касаются внутренним образом в точке A, причем меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
a) Докажите, что прямые KM и BC параллельны.
b) Пусть L — точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC = 16.

Решение похоже на вариант 10.
Точки K и M — середины AB и AC соответственно, т.к. внутренняя окружность проходит через центр внешней и т.к. $\vartriangle AKO \sim \vartriangle ABD$ по двум углам ( $\angle{AKO}= \angle{ABD}=90^{\circ}$ ).
$\Rightarrow KM \parallel BC$ как средняя линия.
Т.к. $KM \parallel BC$ , то дуги PK и PM равны (т.к. $KM \parallel BC$ , то $\angle{BPK}=\angle{PKM}$ как внутренние накрест лежащие).
Т.к. дуги равны, то AP — биссектриса угла CAB, обозначим его за $2\alpha$ .

Т.к. AP — биссектриса, то $\frac{AM}{AK}=\frac{ML}{LK}$

Обозначим $ML=x, LK=k*x, AM=y, AK=k*y$ — по свойству биссектрисы.
Заметим, что $AL*LP=ML*LK$ — по свойству хорд.
Также вспомним формулу длины биссектрисы — $AL^2=AM*AK-ML*LK$ . Обозначим $AL=l$ .
Итак, хорды:

$l^2=kx^2$

и формула длины биссектрисы:

$l^2=ky^2-kx^2$

.
Получаем

$kx^2=ky^2-kx^2$

$y^2=2x^2$

Запишем теорему синусов для $\vartriangle KMA$ :

$\frac{KM}{\sin2\alpha}=\frac{BC/2}{\sin2\alpha}=\frac{(k+1)x}{\sin2\alpha}=\frac{8}{\sin2\alpha}=2r=10$

$\sin2\alpha=\frac{8}{10}=\frac{4}{5}$

$\cos2\alpha=\frac{3}{5}$

Напишем теорему косинусов для $\vartriangle KMA$ :

$KM^2=MA^2+KA^2-2*MA*KA*\cos2\alpha$

$((k+1)*x)^2=(y)^2+(ky)^2-2*y*ky*\cos2\alpha$

$(k+1)^2(x)^2=(y)^2 [1+k^2-2*k*\cos2\alpha]$

Подставим $y^2=2x^2$ и значение $\cos$ :

$(k+1)^2(x)^2=2(x)^2 [1+k^2-2*k*\frac35]$

$(k+1)^2=2 [1+k^2-2*k*\frac35]$

Это квадратное уравнение относительно $k$ , решаем его:

$\left\{ k_1 = \frac{-4 \; \sqrt{6} + 11}{5}, k_2 = \frac{4 \; \sqrt{6} + 11}{5} \right\}$

$x=\frac{KM}{k+1}=\frac{8*5}{\pm4 \sqrt{6} + 16}$

$l^2=kx^2= \frac{8*8*5(\pm4 \sqrt{6} + 11)}{(\pm4 \sqrt{6} + 16)^2}=\frac{8*8*5(\pm4 \sqrt{6} + 11)}{16*6 \pm2*16*4\sqrt{6}+256}=$

$=\frac{8*8*5(\pm4 \sqrt{6} + 11)}{352 \pm128\sqrt{6}}=\frac{8*8*5(\pm4 \sqrt{6} + 11)}{32(11 \pm4\sqrt{6})}=10$

$l=\sqrt{10}$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru