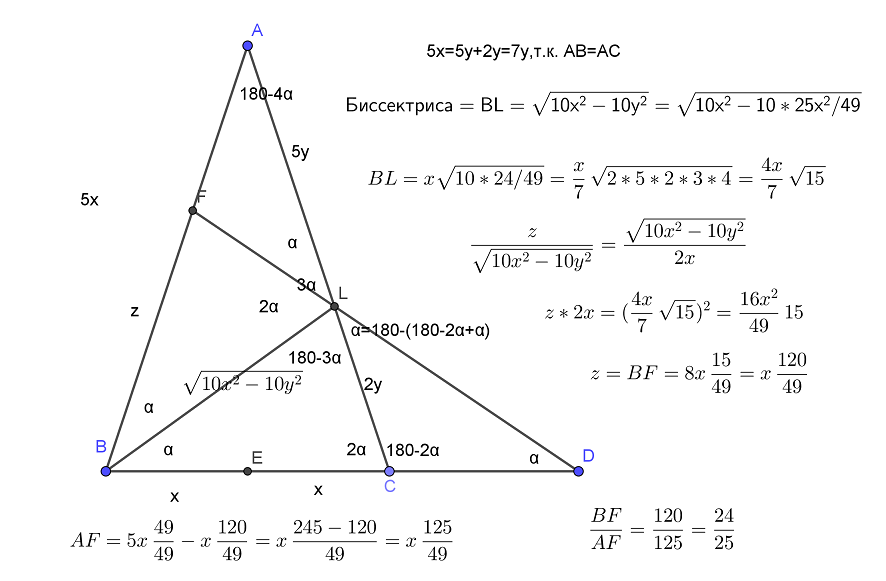
На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что 
. В каком отношении прямая DL делит сторону AB?
Решение смотри на рисунке к задаче.
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru
Спасибо.
1. При построении чертежа необходимо различать «биссектриса угла» и «биссектриса треугольника».
2. При доказательстве опираемся на положение о том, что в равнобедренном треугольнике углы при основании равны.
3. Косинус угла показывает во сколько раз прилежащий катет меньше гипотенузы. Отношение необходимо для применения теоремы о биссектрисе внутреннего угла треугольника.
4 По формуле для вычисления длины биссектрисы вычисляем длину BL
5. Ищем отношение BF к AF
Покажем подобие треугольников BLF и BLC по трем углам.
Подобие позволяет найти коэффициент подобия Для этого вводится переменная z В результате z выражается через x.
Из AB = AF + FB
выражаем АF через х
Теперь находим отношение BF к AF
Это поверхностные комментарии к решению задачи.
2 балла могут не поставить.