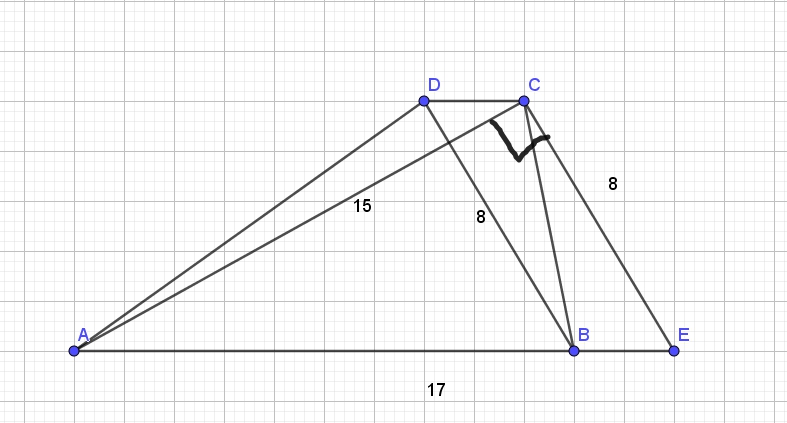
Реальный ЕГЭ 2го июня 2017, задание 16 — Решения вариантов ЕГЭ по математике

Дана трапеция ABCD с диагоналями равными 8 и 15. Сумма оснований трапеции равна 17.
а) Докажите, что диагонали перпендикулярны.
б) Найдите высоту трапеции

Сделаем дополнительное построение — проведем $CE \parallel DB$ . Тогда $CE=DB=8$ , а $DC=BE$ т.к. BECD — параллелограмм.
В треугольнике ACE стороны равны 15, 8, 17, и эти числа удовлетворяют соотношению $15^2+8^2=17^2$ .
Тогда по обратной теореме Пифагора (или по т. косинусов) треугольник $ACE$ — прямоугольный с прямым углом ACE.

Высоту трапеции найдем через общую формулу площади четырехугольника (ABCD)- половина произведения диагоналей на синус угла между ними (угол между диагоналями, очевидно, тоже прямой).

$S(ABCD)=\frac12*15*8*\sin{90^o}=60$

C другой стороны площадь трапеции — полусумма оснований на ее высоту:

$S(ABCD)=\frac12*17*h=60$

$h=\frac{120}{17}$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru