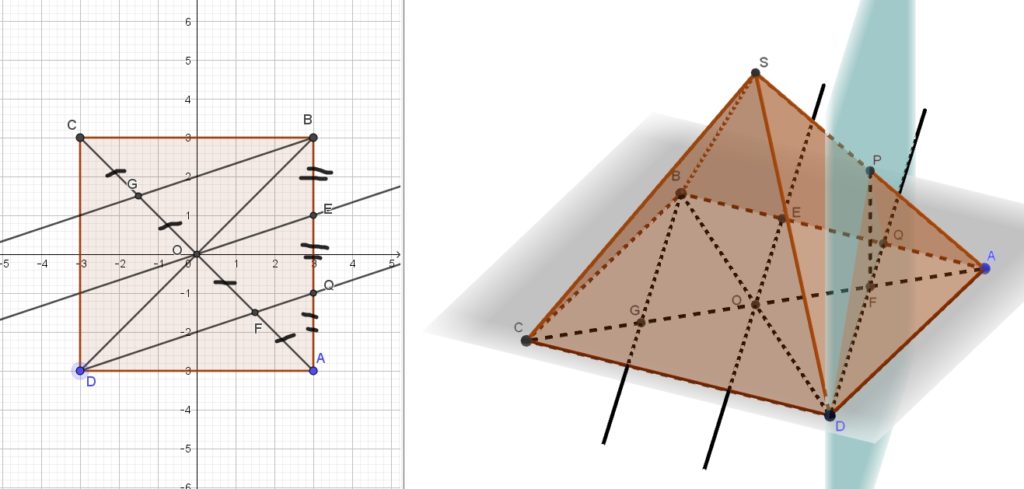
Реальный ЕГЭ 26го июня 2018, задание 14 — Решения вариантов ЕГЭ по математике

В правильной 4х-угольной пирамиде $SABCD$ $AQ:QB=1:2$ , $P$ -середина $AS$
a) Докажите, что плоскость $(DPQ)$ перпендикулярна плоскости основания
b) Найдите площадь сечения $DPQ$ если площадь $DSB$ =6

Проведем диагональ CA, поделим ее на 4 равные части. Возьмем на диагонали три равных отрезка $GO=OF=FA$ . Возьмем на стороне $AB$ три равных отрезка $BE=EQ=QA$ . Очевидно, из подобия соответствующих треугольников, прямые $GB \parallel OE \parallel FQ$
Итак, т. $F$ оказалась серединой $OA$ . Соединим точки $P$ и $F$ . Т.к. $F$ — середина $OA$ , а $P$ — середина $SA$ , то $SO \parallel PF$ . Но т.к. пирамида правильная, то $SO \perp (ABC)$ , значит и $PF \perp (ABC)$ .
Получается, что наша плоскость $(DPQ)$ , которая, очевидно, содержит в себе отрезок $PF$ , проходит через перпендикуляр $PF$ к плоскости основания. Тогда (есть соответствующая теорема) плоскости $(DPQ)$ и основания $(ABC)$ — перпендикулярны.

Найдем, во сколько раз отличаются площади треугольников $DSB$ =6 и $DPQ$ . Их высоты $SO$ и $PQ$ отличаются в 2 раза.
Найдем, во сколько раз отличаются их основания $DB$ и $DQ$ . Пусть $AQ=x$ , тогда $DB=3x\sqrt{2}$ , а $DQ=\sqrt{x^2+(3x)^2}=x\sqrt{10}$
Тогда отношение

$\frac{DB}{DQ}=\frac{3x\sqrt{2}}{x\sqrt{10}}=\frac{3}{\sqrt{5}}$

Тогда искомое отношение площадей

$\frac{S(DSB)}{S(DPQ)}=2*\frac{3}{\sqrt{5}}=\frac{6}{\sqrt{5}}$

и площадь треугольника $DPQ=\sqrt{5}$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru