Решение задания 14.1, Ященко 20 вариантов, ЕГЭ-2019, подготовительные задания

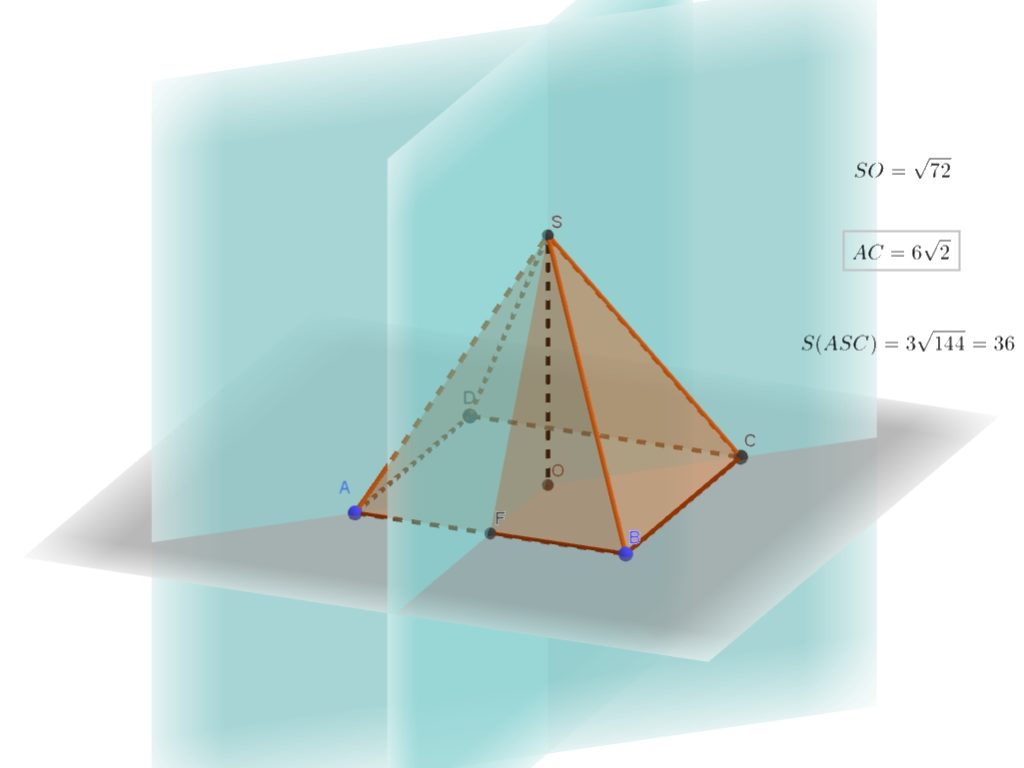
1. Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 108,
а площадь полной поверхности этой пирамиды равна 144.
а) Докажите, что плоскость SAC и плоскость, проходящая через вершину S, середину сто-
роны АВ и центр основания, пересекаются по прямой, содержащей высоту пирамиды.
6) Найдите площадь сечения пирамиды плоскостью SAC.

144-108=36 — площадь основания
6 — сторона основания (сторона квадрата, например AB)
— площадь бокового треугольника =
апофема SF = 9