В правильной треугольной призме стороны основания равны 3, боковые рёбра равны 1, точка D — середина ребра . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и . Решение аналогично варианту 15. Посмотрите решение Читать далее …
Рубрика: Задание 14 (стереометрия)
Решение задания 14, вариант 15, Ященко 36 вариантов, ЕГЭ-2018
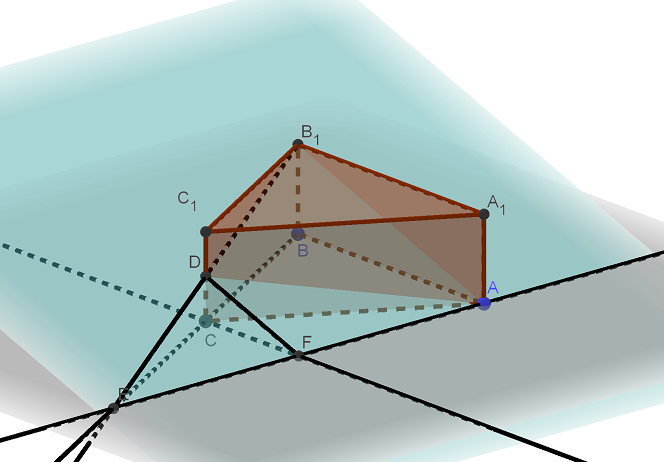
В правильной треугольной призме стороны основания равны 5, боковые рёбра равны 2, точка D — середина ребра . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и . Трехмерная картинка, которую можно крутить в Читать далее …
Решение задания 14, вариант 14, Ященко 36 вариантов, ЕГЭ-2018
В правильной четырёхугольной призме стороны основания равны 3, а боковые рёбра равны 4. На ребре отмечена точка Е так, что . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и Решение похоже на вариант Читать далее …
Решение задания 14, вариант 13, Ященко 36 вариантов, ЕГЭ-2018
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами и . Длины боковых рёбер пирамиды . а) Докажите, что SA — высота пирамиды. б) Найдите угол между прямыми SC и BD. Решение похоже на вариант 9 Трехмерная картинка, которую Читать далее …
Решение задания 14, вариант 12, Ященко 36 вариантов, ЕГЭ-2018
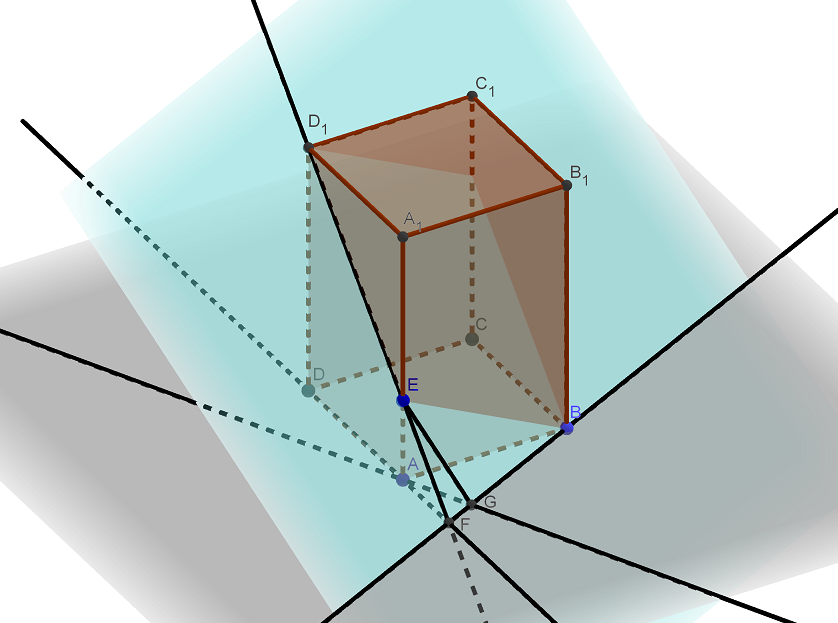
В правильной четырехугольной призме стороны основания равны 2, а боковые ребра равны 3. На ребре отмечена точка E так, что . а) Постройте прямую пересечения плоскостей ABC и . б) Найдите угол между плоскостями ABC и . Трехмерная картинка, которую Читать далее …
Решение задания 14, вариант 11, Ященко 36 вариантов, ЕГЭ-2018
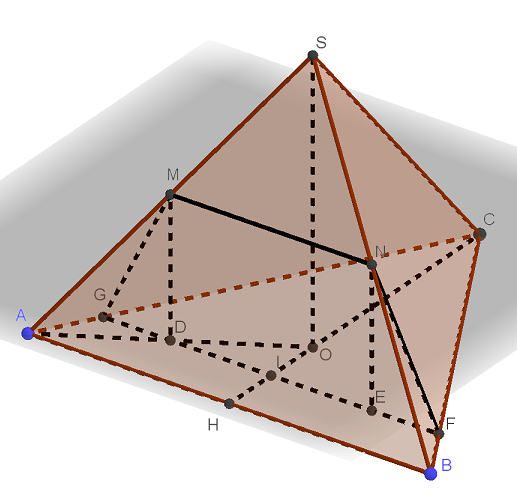
В правильной треугольной пирамиде SABC сторона основания АВ равна 6, а боковое ребро SA равно 4. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
Решение задания 14, вариант 10, Ященко 36 вариантов, ЕГЭ-2018
В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а боковое ребро SA равно 8. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
Решение задания 14, вариант 9, Ященко 36 вариантов, ЕГЭ-2018
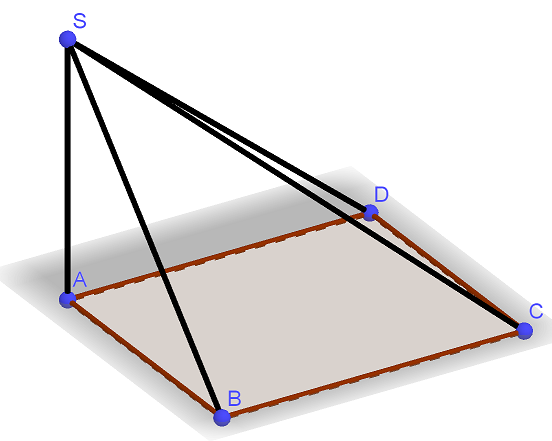
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами и . Длины боковых рёбер пирамиды . а) Докажите, что SA — высота пирамиды. б) Найдите угол между прямой SC и плоскостью ASB. Трехмерная картинка, которую можно крутить в 3D, Читать далее …
Решение задания 14, вариант 8, Ященко 36 вариантов, ЕГЭ-2018
В кубе все рёбра равны 5. На его ребре отмечена точка K так, что KB = 4. Через точки K и построена плоскость , параллельная прямой . а) Докажите, что , где P — точка пересечения плоскости с ребром . Читать далее …
Решение задания 14, вариант 7, Ященко 36 вариантов, ЕГЭ-2018
В правильной треугольной пирамиде SABC сторона основания АВ равна 12, а боковое ребро SA равно 13. Точки М и N — середины рёбер SA и SB соответственно. Плоскость содержит прямую MN и перпендикулярна плоскости основания пирамиды. а) Докажите, что плоскость Читать далее …
Решение задания 14, вариант 6, Ященко 36 вариантов, ЕГЭ-2018
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а . а) Докажите, что эта пирамида правильная. б) На рёбрах DA и DC отмечены точки M и N соответственно, причём . Найдите площадь сечения MNB. Решение аналогично варианту 4
Решение задания 14, вариант 5, Ященко 36 вариантов, ЕГЭ-2018
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а . а) Докажите, что эта пирамида правильная. б) На рёбрах DA и DC отмечены точки M и N соответственно, причём . Найдите площадь сечения MNB. Решение аналогично варианту 4
Решение задания 14, вариант 4, Ященко 36 вариантов, ЕГЭ-2018
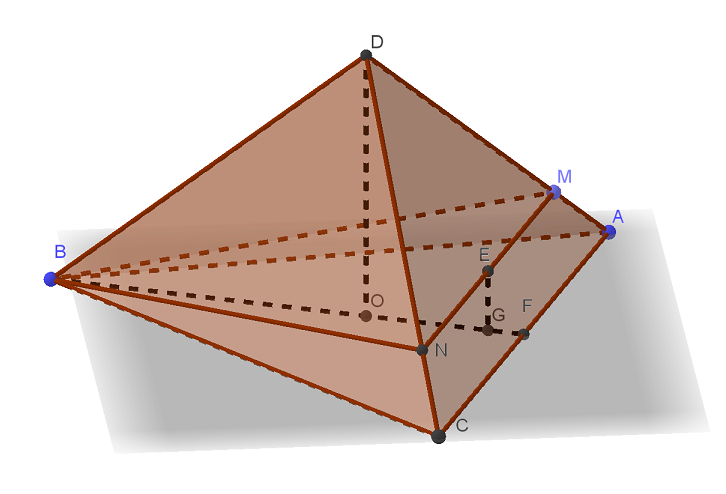
В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB = BC = AC = 14. а) Докажите, что эта пирамида правильная. б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA = DN:NC Читать далее …
Решение задания 14, вариант 3, Ященко 36 вариантов, ЕГЭ-2018
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM:МА =3:4. Точки P и Q — середины рёбер ВС и AD соответственно. а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией. б) Найдите отношение Читать далее …
Решение задания 14, вариант 2, Ященко 36 вариантов, ЕГЭ-2018
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM:МА =1:2. Точки P и Q — середины рёбер ВС и AD соответственно. а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией. б) Найдите отношение Читать далее …
Решение задания 14, вариант 1, Ященко 36 вариантов (профиль), ЕГЭ-2018. Ответ.
На ребре SA правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка М, причём SM : МА = 5:1. Точки P и Q — середины рёбер ВС и AD соответственно. а) Докажите, что сечение пирамиды плоскостью MPQ является равнобедренной трапецией. Читать далее …
Решение задания 14, вариант 19, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 21, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 25, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 24, Ященко 36 вариантов, ЕГЭ-2017
Читаем Погорелова на стр. 282 https://yadi.sk/d/VB_dPOI43GYVLn — нам нужно провести из т. B перпендикуляр на прямую SA — получим точку E и из этой точки восстанавливаем второй перпендикуляр к линии пересечения плоскостей — уже во второй плоскости Открыть на полную Читать далее …
Решение задания 14, вариант 26, Ященко 36 вариантов, ЕГЭ-2017
Открыть на полную страницу: cсылка .
Решение задания 14, вариант 33, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 20, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 22, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 34, Ященко 36 вариантов, ЕГЭ-2017
Открыть на полную страницу: cсылка .
Решение задания 14, вариант 27, Ященко 36 вариантов, ЕГЭ-2017
В тр. B1KC1 правой грани опустим высоту из т. B1 на прямую C1K Получим точку J. Соединим точку J с точкой P. Докажем, что плоскость PJB1 ⊥ прямой KC1 и тогда угол PJB1 — искомый линейный угол двугранного угла между Читать далее …
Решение задания 14, вариант 23, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 28, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 29, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 30, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 31, Ященко 36 вариантов, ЕГЭ-2017
Возьмем т.H — середину AB. Проведем OH. Тогда OH ⊥ AB (OAB — равнобедренный тр) Проведем SH. Докажем, что SH⊥AB. Действительно, AB⊥SO и AB⊥OH ⇒ AB⊥плоскости SOH и AB⊥SH как лежащей в этой плоскости Проведем OK — высоту в тр Читать далее …
Решение задания 14, вариант 32, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 35, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 36, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 14, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 15, Ященко 36 вариантов, ЕГЭ-2017
Решение задания 14, вариант 17, Ященко 36 вариантов, ЕГЭ-2017
Открыть на полную страницу: cсылка .