Реальный ЕГЭ 29 мая 2019, задание 15 — Решения вариантов ЕГЭ по математике

$\log_{3}{(5-5x)} \geq \log_{3}{(x^2-3x+2)} -\log_{3}{(x+4)}$

$\log_{3}{ \Big( (5-5x)(x+4)\Big) } - \log_{3}{(x^2-3x+2)} \geq 0$

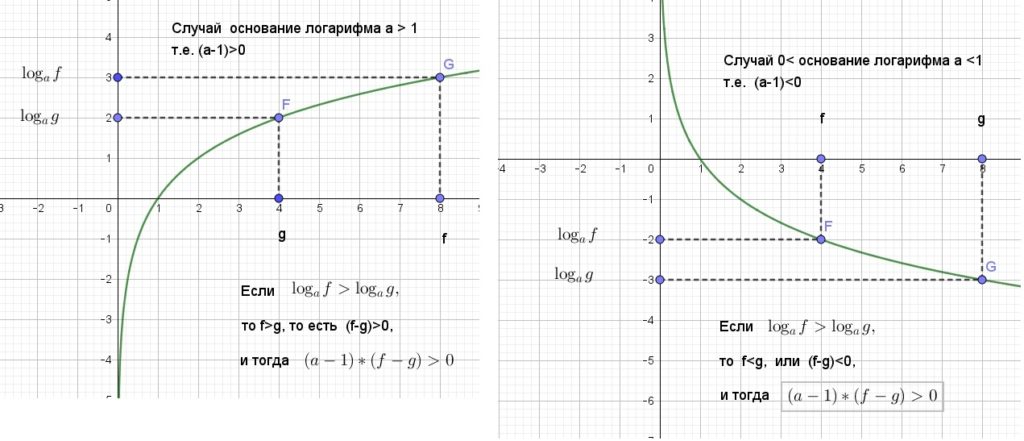
По методу замены множителей (см. учебник Ериной, стр 313 ) следующая функция будет иметь те же знаки на тех же интервалах (но каждая на своем ОДЗ):

$(3-1)* \Big( (5-5x)(x+4) - (x^2-3x+2) \Big) \geq 0$

$2* \Big( 5x-5x^2-20x+20-x^2+3x-2 \Big) \geq 0$

$( -6x^2-12x+18 ) \geq 0$

$-6(x+3)(x-1) \geq 0$

т.е.

(1) $\begin{equation*} x \in [-3; 1] \end{equation*}$

Теперь найдем ОДЗ:

$\begin{Bmatrix}{ 5-5x > 0 }\\{x+4>0}\\{ x^2-3x+2 >0 }\end{matrix}$

$\begin{Bmatrix}{ x<1 }\\{x>-4}\\{ (x<1) \bigcup (x>2) }\end{matrix}$

т.е.

(2) $\begin{equation*} x \in (-4;1) \end{equation*}$

Пересечем интервалы (1) и (2) получим ответ: $[-3;1)$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru