Досрочный ЕГЭ по профильной математике от 27 марта 2023

Павел Коваленко
    1. Острый угол 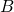B прямоугольного треугольника
      равен 66∘. Найдите угол между высотой CH
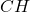      и медианой 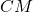CM , проведёнными из вершины
      прямого угла. Ответ дайте в градусах.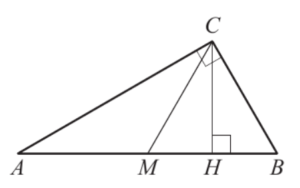

    2. Найдите объём многогранника, вершинами
      которого являются точки A, D, A_1, B, C, B_1
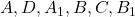      прямоугольного параллелепипеда
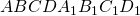      ABCDA_1B_1C_1D_1, у которого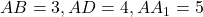 AB=3,AD=4,AA_1=5

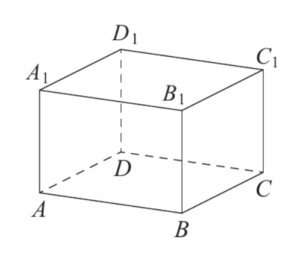
    3. В случайном эксперименте симметричную монету бросают дважды. Найдите
      вероятность того, что орел выпадет ровно один раз.

    4. В торговом центре два одинаковых автомата продают жвачку. Вероятность
      того, что к концу дня в автомате закончится жвачка, равна 0,4. Вероятность
      того, что жвачка закончится в обоих автоматах, равна 0,2. Найдите
      вероятность того, что к концу дня жвачка останется в обоих автоматах.

    5. Найдите корень уравнения \sqrt{19 + 5x} = 2

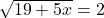
    6. Найдите значение выражения \sqrt{48}*\cos^2{\frac{19\pi}{12}}-\sqrt{12}

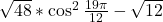
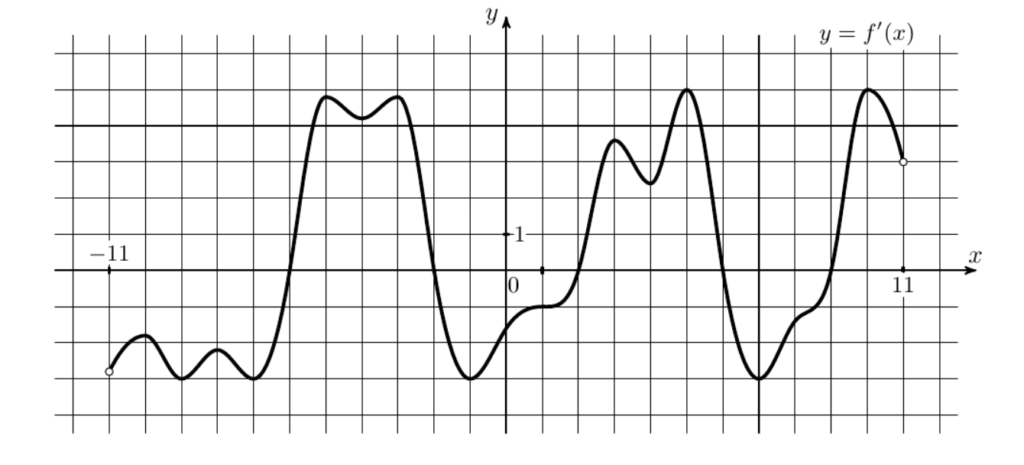
    7. На рисунке изображён график 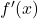f'(x) — производной функции 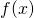f(x), определённой на интервале 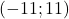(-11; 11). Найдите количество точек экстремума функции 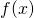f(x), принадлежащих отрезку [-10; 10].

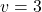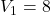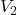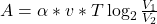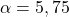    8. Водолазный колокол, содержащий в начальный момент времени v = 3 моля воздуха объёмом V_1 = 8 л, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного объёма V_2 Работа, совершаемая водой при сжатии воздуха, определяется выражением  A=\alpha*v*T\log_2{\frac{V_1}{V_2}} , где \alpha= 5,75  Дж/(моль·К) — постоянная, а 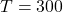T= 300 К температура воздуха. Найдите, какой объём 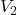V_2 (в литрах) станет занимать воздух, если при сжатии воздуха была совершена работа в 10350 Дж.

    9. Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?

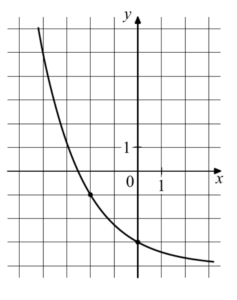
    10. На рисунке изображён график функции f(x) =a^x+b. Найдите f(-8).
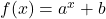    11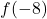. Найдите точку минимума функции y=x^3 - 3x^2 + 2

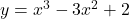
    12. а) Решите уравнение

          \[\log_3(\cos(\frac{\pi}{2}-x) + \sin(2x) + 81) = 4\]

      б) Укажите корни этого уравнения, принадлежащие отрезку [-\frac{7\pi}{2};-2\pi].

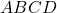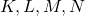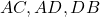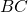    13. Дан тетраэдр ABCD. Точки K,L,M,N лежат на ребрах AC, AD, DB и BC соответственно, так, что четырехугольник 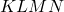KLMN квадрат со стороной 2.   AK:KC = 2 : 3
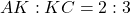      a) Докажите, что BM:MD = 2 : 3
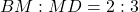      б) Найдите расстояние от точки С до плоскости 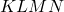KLMN , если объем
      тетраэдра равен 25

    14. Решите неравенство

          \[\frac{4^x+2^{x+1}-36}{2^x-5}+\frac{4^{x+1}-2^{x+5}+4}{2^x-8} \le 5*2^x+7\]

    15. В июле 2020 года планируется взять кредит в банке на некоторую сумму.
      Условия его возврата таковы:
      – каждый январь долг увеличивается на 25% по сравнению с концом
      предыдущего года;
      – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
      Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 65 500 рублей больше суммы, взятой в кредит?

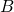    16. Точка B лежит на отрезке 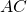AC . Прямая, проходящая через точку 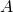A, касается окружности с диаметром 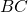BC в точке 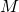M и второй раз пересекает окружность с диаметром 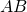AB в точке 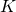K. Продолжение отрезка 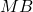MB пересекает окружность с диаметром 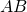AB в точке D.
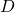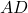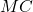      а) Докажите, что прямые AD и MC параллельны.
      б) Найдите площадь треугольника 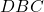DBC, если 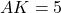AK= 5 и KM= 25

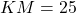
    17. Найдите все значения a, при каждом из которых уравнение

          \[\sqrt{1-2x}*\ln(25x^2-a^2)=\sqrt{1-2x}*\ln(5x-a)\]

      имеет ровно один корень.

    18. Дано натуральное число. К этому числу можно либо прибавить утроенную
      сумму его цифр, либо вычесть утроенную сумму его цифр. После
      прибавления или вычитания суммы цифр, число должно остаться
      натуральным.
      a) Можно ли получить из число 128 число 29?
      б) Можно ли получить из число 128 число 31?
      в) Какое наименьшее число можно было получить из числа 128?

Нашел на просторах интернета уже записанное видео с решением этих задач:



Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru