Найти все значения a, при каждом из которых система уравнений
![]()
имеет более одного решения.
Раскроем модуль:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} { \begin{Bmatrix} {x^2+y^2-25 \ge 0} \\{x^2+20x+y^2-20y+75=x^2+y^2-25} \\{x-y=a} \end{matrix} }\\ { \begin{Bmatrix} {x^2+y^2-25 < 0} \\{x^2+20x+y^2-20y+75=-x^2-y^2+25} \\{x-y=a} \end{matrix} } \end{matrix}\]](https://ege-resheniya.ru/wp-content/ql-cache/quicklatex.com-8e3e751ef29cb29c0ec2a2b1f378def1_l3.png)
![Rendered by QuickLaTeX.com \[\begin{bmatrix} { \begin{Bmatrix} {x^2+y^2 \ge 5^2} \\{y=x+5} \\{y=x-a} \end{matrix} }\\ { \begin{Bmatrix} {x^2+y^2 < 5^2} \\{x^2+10x+y^2-10y+25+25=25} \\{y=x-a} \end{matrix} } \end{matrix}\]](https://ege-resheniya.ru/wp-content/ql-cache/quicklatex.com-a52ceadd5c8f0216724f70930df27a4f_l3.png)
![Rendered by QuickLaTeX.com \[\begin{bmatrix} { \begin{Bmatrix} {x^2+y^2 \ge 5^2} \\{y=x+5} \\{y=x-a} \end{matrix} }\\ { \begin{Bmatrix} {x^2+y^2 < 5^2} \\{ (x+5)^2 +(y-5)^2 =5^2} \\{y=x-a} \end{matrix} } \end{matrix}\]](https://ege-resheniya.ru/wp-content/ql-cache/quicklatex.com-b7d10ce004cb3b44373e5db8564bf6f1_l3.png)

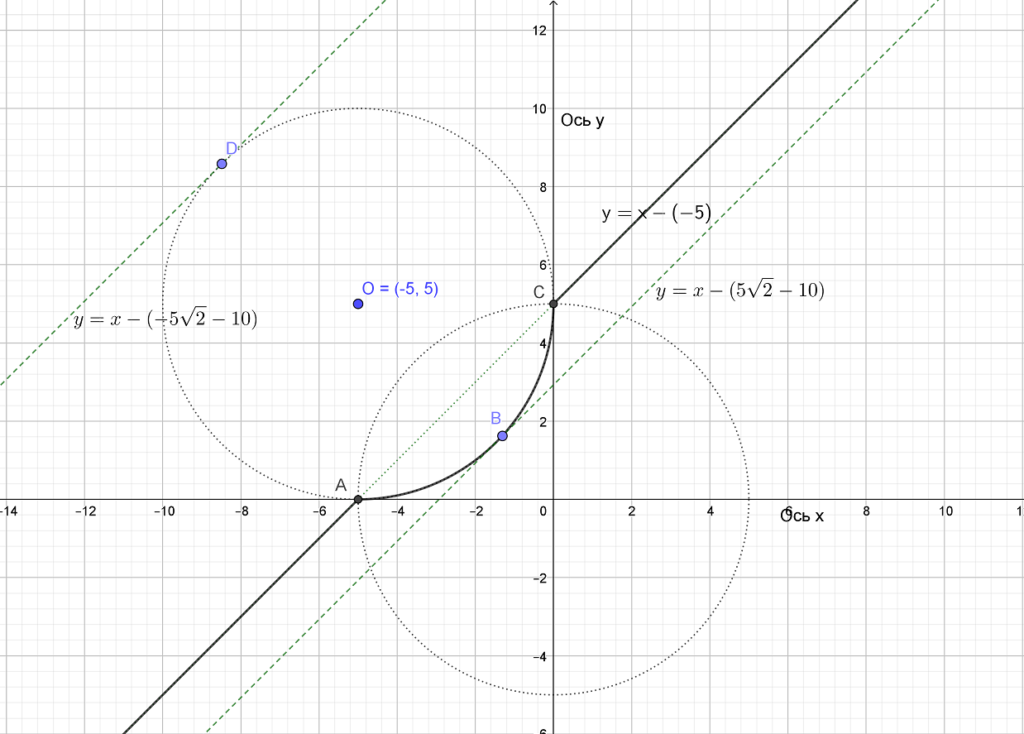
Найдем значение параметра ![]() при котором прямая
при котором прямая ![]() касается окружности
касается окружности ![]() с центром O(-5,5), для этого подставим
с центром O(-5,5), для этого подставим ![]() вместо
вместо ![]() в окружность, получим:
в окружность, получим:
![]()
![]()
Касание будет, когда у этого уравнения всего одно решение, т.е. при дискриминанте равном нулю:
![]()
Получаем:
![]()
![]()
При значениях параметра ![]() между
между ![]() и
и ![]() дискриминант будет положителен — значит будет два пересечения прямой и окружности. При значениях параметра
дискриминант будет положителен — значит будет два пересечения прямой и окружности. При значениях параметра ![]() равных
равных ![]() и
и ![]() — корень у
— корень у ![]() только один — происходит касание прямой
только один — происходит касание прямой ![]() и окружности
и окружности ![]()
Нам подходят все значения параметра ![]() , при которых прямая
, при которых прямая ![]() пересекает окружность между точками
пересекает окружность между точками ![]() и
и ![]() .
.
Плюс также вы можете посмотреть решение в самой книжке Ященко на стр.215. Нажмите на ссылку.
Ответ: Исходная система имеет более одного решения при ![]()
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru


