Найти все значения ![]() , при каждом из которых уравнение
, при каждом из которых уравнение ![]() имеет единственный корень.
имеет единственный корень.
Введем новый параметр ![]() и перепишем в виде
и перепишем в виде ![]() или
или
![]()
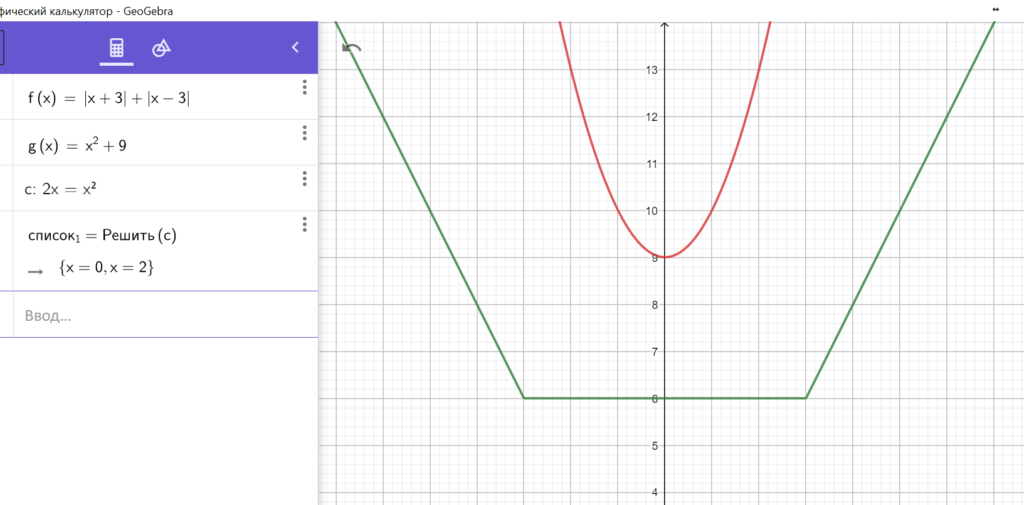
Заметим, что при изменении ![]() у нас слева парабола ездит вверх-вниз, а фигура
у нас слева парабола ездит вверх-вниз, а фигура ![]() тоже ездит вверх-вниз и при этом становится уже-шире, с горизонтальной линией на высоте
тоже ездит вверх-вниз и при этом становится уже-шире, с горизонтальной линией на высоте ![]() между точками
между точками ![]() и
и ![]() .
.
В силу симметрии относительно вертикальной оси у нас корни, если они будут, будут симметричны — корню слева от оси OY будет соответствовать корень справа от оси OY — и на той же высоте, при том же значении ![]() . Поэтому нечетное число корней может быть, если корнем является значение
. Поэтому нечетное число корней может быть, если корнем является значение ![]() .
.
Подставим в наше уравнение ![]() — получим:
— получим:
![]()
![]()
![]()
![]()
![]() или
или ![]()
При ![]() будет 3 корня:
будет 3 корня:
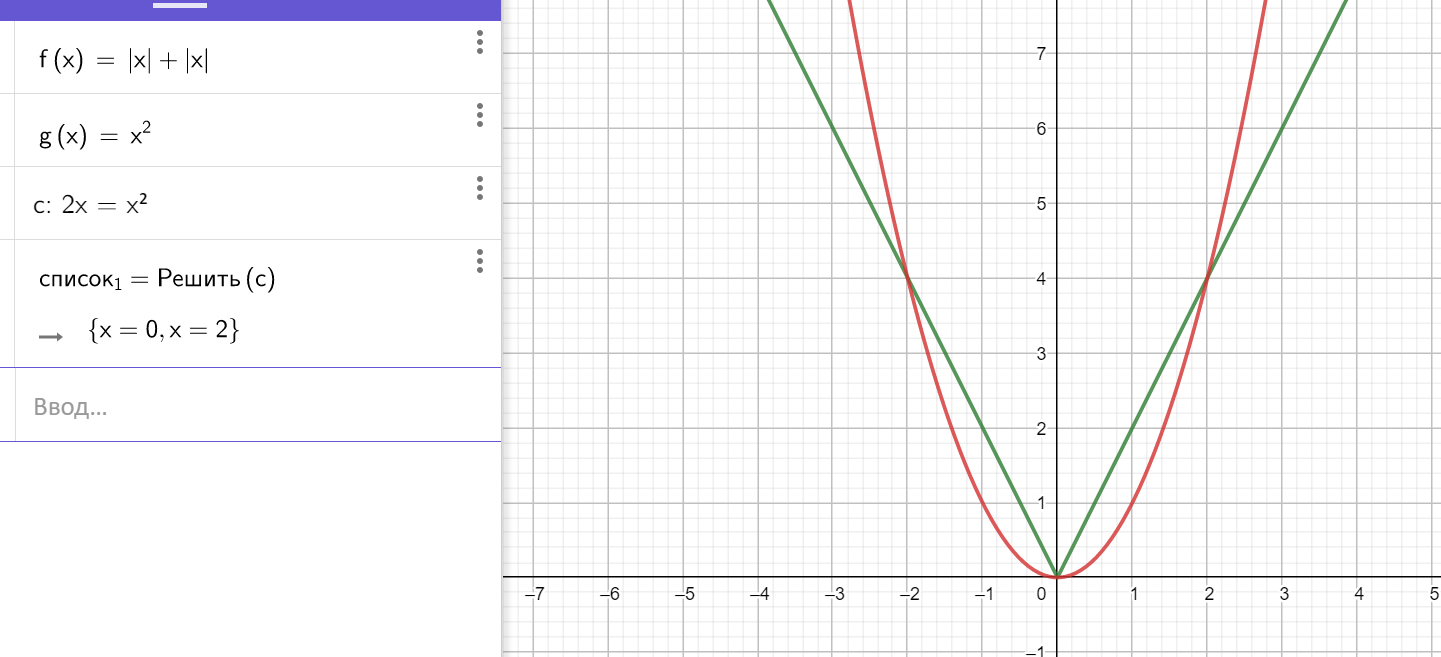
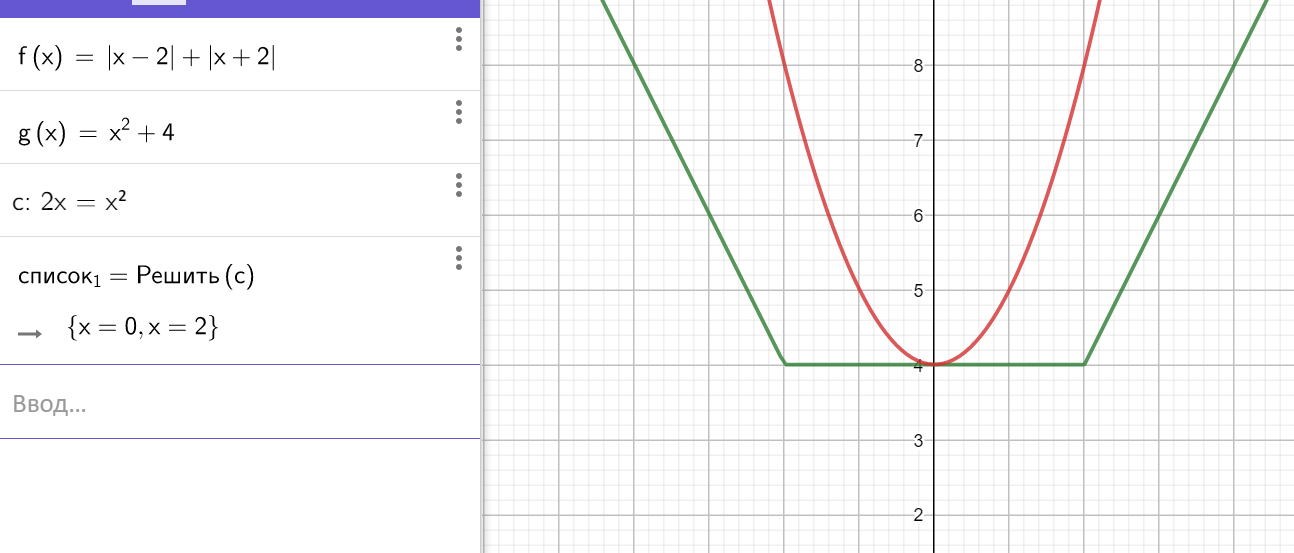
При ![]() и
и ![]() будет один корень
будет один корень ![]() :
:
Осталось перейти от ![]() к
к ![]()
Ответ: ![]() и
и ![]()
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru


