Решение задания 18, вариант 15, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике

Найти все значения $a$ , при каждом из которых система уравнений

$\begin{Bmatrix} {x^2+5x+y^2-y-|x-5y+5|=52} \\{y-2=a(x-5)} \end{matrix}$

имеет ровно два решения.

Раскроем модуль:

$\begin{bmatrix} { \begin{Bmatrix} {x^2+5x+y^2-y-(x-5y+5)=52} \\{x-5y+5 \ge 0} \\{y-2=a(x-5)} \end{matrix} }\\{ \begin{Bmatrix} {x^2+5x+y^2-y+(x-5y+5)=52} \\{x-5y+5 < 0} \\{y-2=a(x-5)} \end{matrix} } \end{matrix}$

$\begin{bmatrix} { \begin{Bmatrix} {x^{2} + y^{2} + 4 \; x + 4 \; y - 5 = 52} \\{y \le \frac{x+5}{5}=\frac{x}{5}+1} \\{y-2=a(x-5)} \end{matrix} }\\{ \begin{Bmatrix} {x^{2} + y^{2} + 6 \; x - 6 \; y + 5 = 52} \\{y> \frac{x+5}{5}=\frac{x}{5}+1} \\{y-2=a(x-5)} \end{matrix} } \end{matrix}$

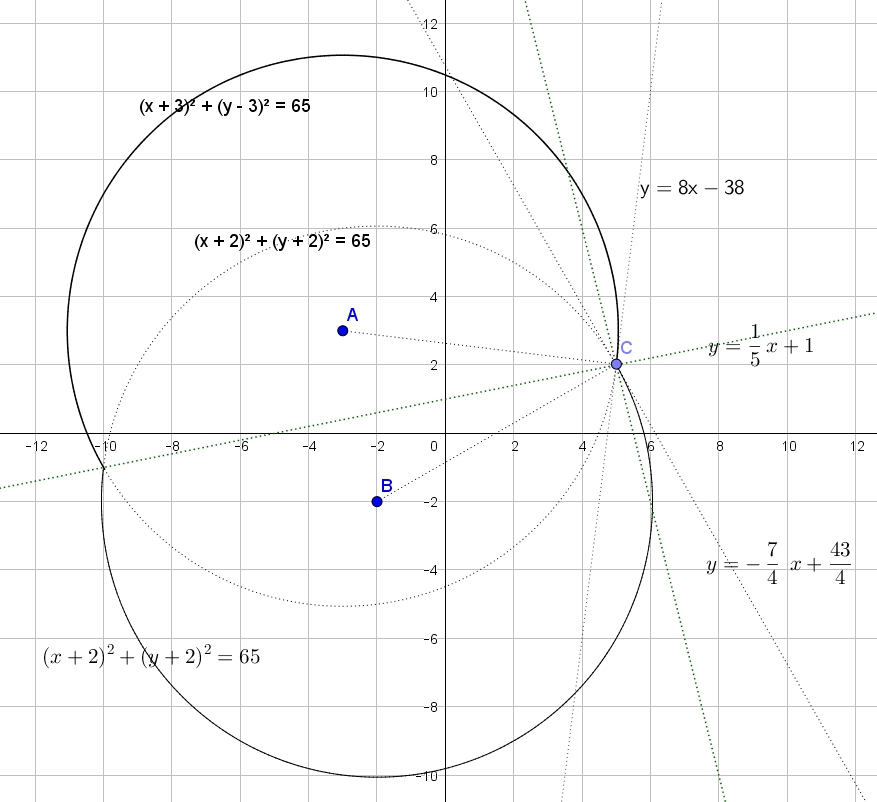
$\begin{bmatrix} { \begin{Bmatrix} {\left(x + 2 \right)^{2} + \left(y +2 \right)^{2} = 65} \\{y \le \frac{x}{5}+1} \\{y-2=a(x-5)} \end{matrix} }\\{ \begin{Bmatrix} {\left(x + 3 \right)^{2} + \left(y - 3 \right)^{2} = 65} \\{y> \frac{x}{5}+1} \\{y-2=a(x-5)} \end{matrix} } \end{matrix}$

Ровно два решения будет, когда когда прямая $y-2=a(x-5)$ в крайних положениях является касательной к окружностям — к одной и ко второй. Тангенс угла наклона касательной проще всего найти из понимания, что касательная перпендикулярна радиусу, проведенному в точку касания, и что перпендикулярные прямые имеют произведение коэффициентов углов наклона, равное $-1$ .
Тангенс угла наклона отрезка $AC = -\frac18$ , значит перпендикулярная ему касательная будет иметь тангенс угла наклона $=8$ . Тангенс угла наклона отрезка $BC = \frac47$ , значит перпендикулярная ему касательная будет иметь тангенс угла наклона $=-\frac74$

Ответ: $a \in [-\frac74; 8]$ .

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru