Решение задания 17, вариант 29, Ященко 36 вариантов, ЕГЭ-2018

В двух шахтах добывают алюминий и никель. В первой шахте имеется 60 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 1 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?

Похожие варианты: 15, 19, 24, 31, 35

Первая шахта : всего 300 человеко-часов
Пусть M — число человеко-часов, потраченных на добычу алюминия в 1й области
Тогда (300-M) — число человеко-часов, потраченных на добычу никеля в 1й области
Тогда 2*M — число добытых килограмм алюминия в 1й области за сутки
Тогда 1*(300-M) — число добытых килограмм никеля в 1й области за сутки
2я область: всего 500 человеко-часов
Пусть N — число человеко-часов, потраченных на добычу алюминия в 2й области
Тогда (500-N) — число человеко-часов, потраченных на добычу никеля в 2й области
Тогда 1*N — число добытых килограмм алюминия в 2й области за сутки
Тогда 2*(500-N) — число добытых килограмм никеля в 2й области за сутки

Масса добытого в сумме в двух областях алюминия за сутки:

   

Масса добытого в сумме в двух областях никеля за сутки:

   

Поскольку у нас в сплаве на 2 кг алюминия должно приходится 1 кг никеля, то у нас есть условие 2:1 , количество кг одного должно равняться удвоенному количеству килограмм другого, это задает строгую связь между и , например 100 кг алюминия = 2 * 50 кг никеля (на 100 кг алюминия приходится 50 кг никеля):

(1)  

Это задает уравнение линии на плоскости :

(2)  

Полная масса сплава из никеля и алюминия за сутки как функция двух переменных :

(3)  

Полная масса сплава зависит и от , и от . Это задает поверхность над координатами (3).
Нам нужен максимум этой функции, максимум поверхности, но при этом на линии, задаваемой уравнением (2) и в рамках прямоугольника 300×500.

Для этого надо взять производную, но у нас две переменных , поэтому выразим через (уравнение (2)) и подставим это в (уравнение (3)). Получим зависимость , т.е. только от одной переменной :

   

   

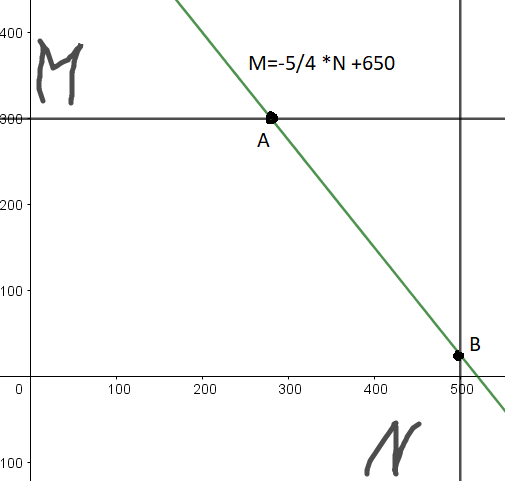
Т.к. производная отрицательна, то функция максимальна на левом конце отрезка. Но фишка в том, что у нас на самом деле находится не в пределах [0,500], а в пределах [280,500] — это хорошо видно на рисунке — наши границы — это не весь прямоугольник, а мы живем на линии ограничения 2:1, поэтому мы живем между точками A и B, и нам нужно найти левую границу — координаты точки A. Они легко находятся, если подставить в наше ограничение 2:1 (уравнение (2) ) значение граничное . Отсюда и точка A имеет координаты
Подставляем координаты точки A в функцию F(M,N) и получаем ответ: