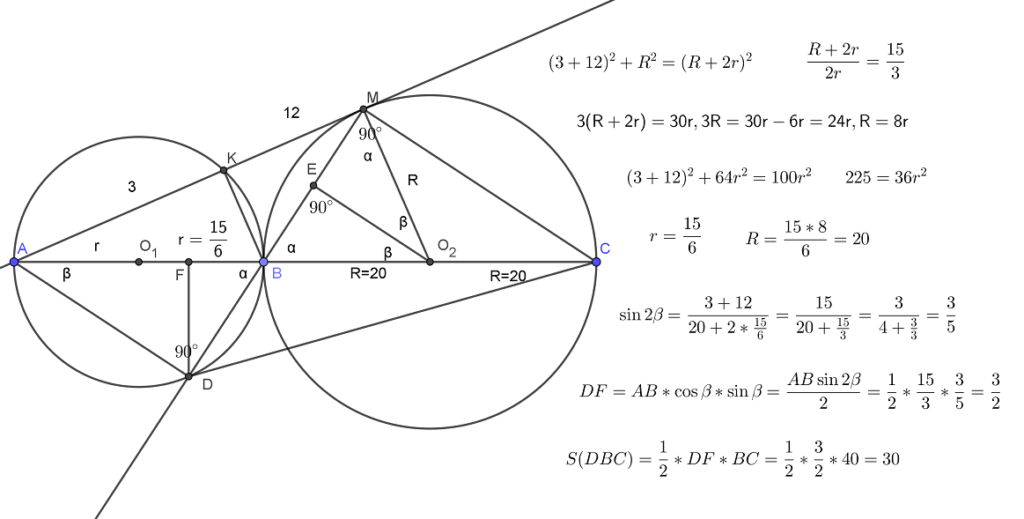
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 3 и MK = 12.
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru



Площади треугольников DBC и АВМ равны как как разности равновеликих (с общим основанием и высотой) ADC и ADM и общего ADC. По свойству касательной и секущей, проведенных из одной точки к окружности и из подобия прямоугольных треугольников с общим углом А имеем AM*AM = AB* AC, AB* 9AB = 15*15, AB = 5. Тогда из прямоугольного АВК по теореме Пифагора имеем ВК = 4. S(DBC)= S(ABK) = (15*4):2 =30.