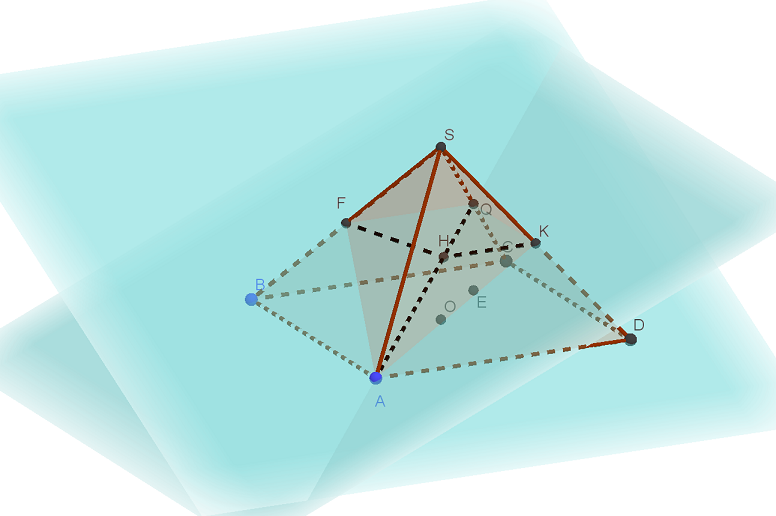
Решение задания 14, вариант 26, Ященко 36 вариантов, ЕГЭ-2018

Павел Коваленко

В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, G(она же Q) — середина ребра SC.
а) Постройте прямую пересечения плоскостей ABQ и QDF.

б) Найдите угол между плоскостями ABQ и QDF.

Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/bHhPGjmT

План решения.
Угол между плоскостями ABQ и QDF найдем из треугольника FHK по теореме косинусов. Для этого надо вычислить стороны треугольника FHK. FH=HK найдем как высоты в треугольниках AFQ и AKQ через их площадь. А их площадь найдем через синусы углов AFQ и AKQ. А синусы найдем через косинусы.

    \[SO^2=(1)^2-(\frac{\sqrt{2}}{2})^2=\frac12\]

    \[AQ^2=(\frac34*\sqrt{2})^2+(\frac12*SO)^2=\frac{9}{16}*2+\frac14*\frac12=\frac54\]

    \[\cos\angle AFQ=\frac{AQ^2-AF^2-FQ^2}{-2*AF*FQ}=\frac{ \frac54-\frac34-\frac14 }{-2*\frac{\sqrt{3}}{2} *\frac12}=-\frac{1}{2\sqrt{3}}\]

    \[\sin \angle AFQ =\sqrt{1-\frac{1}{12}}=\sqrt{\frac{11}{12}}\]

    \[S(\triangle AFQ)=\frac12*AF*FQ*\sin \angle AFQ=\frac12* \frac{\sqrt{3}}{2}*\frac12*\sqrt{\frac{11}{12}}=\frac{\sqrt{11}}{16}\]

С другой стороны,

    \[S(\triangle AFQ)=\frac12*FH*AQ=\frac12*FH*\frac{\sqrt{5}}{2}\]

Откуда:

    \[\frac{\sqrt{11}}{16} =\frac12*FH*\frac{\sqrt{5}}{2}\]

    \[FH=HK=\frac{\sqrt{11}}{4\sqrt{5}}\]

    \[FK=\frac{\sqrt{2}}{2}\]

По теореме косинусов:

    \[\cos \angle FHK= \frac{FK^2-FH^2-HK^2}{-2*FH*HK}=\frac{\frac12-\frac{11}{80}-\frac{11}{80}}{-2\frac{11}{5*16} }=\frac{\frac{9}{40}}{-\frac{11}{40} }=-\frac{9}{11}\]

Но этот угол тупой, т.е. больше 90^o, т.к. косинус отрицательный.
Нам нужен острый угол, который есть 180^o минус этот угол.
Косинусы смежных углов имеют разные знаки.
Значит косинус острого угла = \frac{9}{11}
Ответ: arccos\frac{9}{11}



Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru

2 комментария к “Решение задания 14, вариант 26, Ященко 36 вариантов, ЕГЭ-2018”

  1. Где точка G на рисунке?????? Может не Q, а G?????

    1. Да, правильно, опечатка , G=Q

Комментарии закрыты.