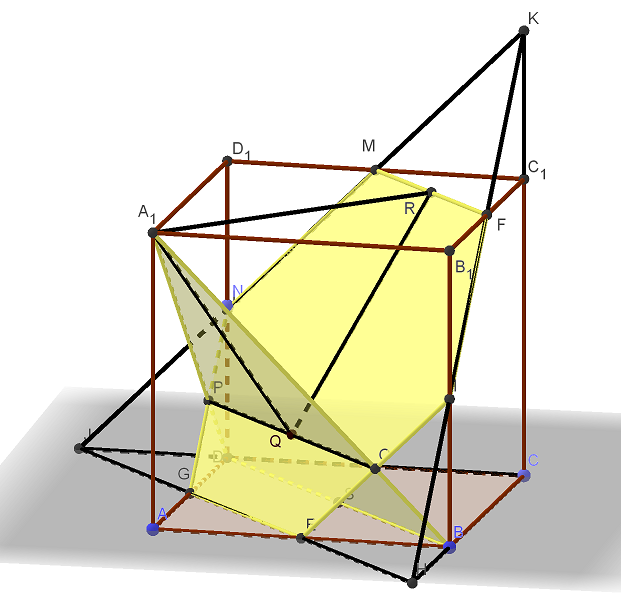
Решение задания 14, вариант 21, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике

Дан куб $ABCDA_1B_1C_1D_1$ .

а) Постройте сечение куба плоскостью, проходящей через середины его рёбер $AB, B_1C_1, AD$ .

б) Найдите угол между плоскостью $A_1BD$ и плоскостью, проходящей через середины рёбер $AB, B_1C_1, AD$ .

Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке
https://ggbm.at/nAKXHwEB

Пусть $a$ — ребро куба.

$A_1R=\frac34 a\sqrt{2}$

$A_1Q=\frac34*a\sqrt{2}*\frac{\sqrt{3}}{2}=\frac34 a\sqrt{\frac32}$

$RQ=\frac34 C_1S=\frac34*\sqrt{a^2+(\frac{a\sqrt{2}}{2})^2}=\frac34 a\sqrt{\frac32}$

По теореме косинусов

$A_1R^2=A_1Q^2+RQ^2-2A_1Q*RQ*\cos\angle A_1QR$

$\frac{9}{16}*2=2*\frac{9}{16}*\frac32- 2 *\frac{9}{16}*\frac32*\cos\angle A_1QR$

$\cos\angle A_1QR =\frac{2-3}{-3}=\frac13$

$tg \angle A_1QR = \sqrt{3^2-1}=2\sqrt{2}$

Второй способ.
Введем систему координат $B(0;0;0), D(2;2;0), A_1(0;2;2), I(0;0;1), E(0;1;0), F(1;0;2)$
Уравнение плоскости, проходящей через $B,D,A_1$ :

$Ax+By+Cz+D=0$

Подставляем в него точки $B,D,A_1$ :

$D=0$

$2A+2B=0 => A=-B$

$2B+2C=0 => C=-B=A$

Можно взять $A=1=C; B=-1; D=0$
Получаем уравнение плоскости, проходящей через $B,D,A_1$ :

$x-y+z+0=0$

Вектор, перпендикулярный плоскости $(BDA_1)$ , имеет координаты (1;-1;1)

Уравнение плоскости, проходящей через $I,E,F$ :

$A'x+B'y+C'z+D'=0$

Подставляем в него точки $I,E,F$ :

$C'+D'=0 => C'=-D'$

$B'+D'=0 => B'=-D'=C'$

$A'+2C'+D'=0$

$A'=-D'-2C'=C'-2C=-C'$

Можно взять $A'=-1; B'=C'=1; D'=-1$
Получаем уравнение плоскости, проходящей через $I,E,F$ :

$-x+y+z-1=0$

Вектор, перпендикулярный плоскости $(IEF)$ , имеет координаты (-1;1;1)

Возьмем скалярное произведение векторов $(1;-1;1)*(-1;1;1)=-1-1+1=-1$
C другой стороны оно равно произведению длин этих векторов на косинус угла между ними:

$-1=\sqrt{3}*\sqrt{3}*\cos\phi$

Откуда

$\cos\phi=-\frac13$

Знак минус означает, означает, что угол тупой, но нам нужен острый, поэтому
Ответ: $\cos\phi=\frac13$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru