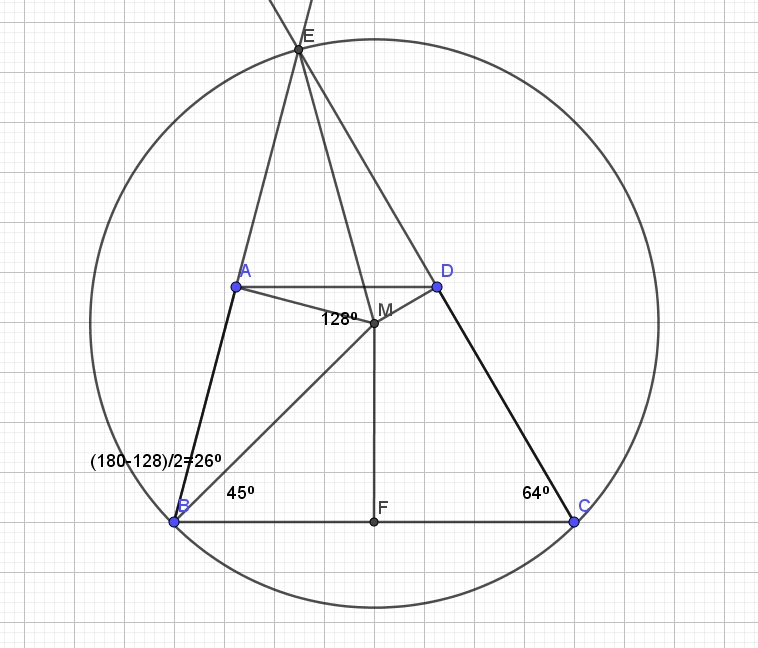
В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку M так, что углы BAM и CDM — прямые.
a) Докажите, что BM=CM
b) Найдите угол ABC, если угол BCD=64 градуса, а расстояние от точки М до прямой BC равно стороне AD.
Решение
a) Это очевидно, если заметить, что центр описанной окружности лежит на пересечении серединных перпендикуляров, и AD — средняя линия в тр. BEC
b) Угол BCD — вписанный, ему соответствует центральный угол BME =128 градусов, и в равностороннем тр BME находим угол EBM = 26 гр.
Угол MBF = 45 градусов , т.к. MF=BF=AD (F — середина BC, и FM — серединный перпендикуляр)
Ответ: 45+26=71 градус
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru


