Найти все значения ![]() , при каждом из которых система уравнений
, при каждом из которых система уравнений
![]()
имеет более двух решений.
Раскроем модуль:
![Rendered by QuickLaTeX.com \[\begin{bmatrix} { \begin{Bmatrix} {(x^2-1)+2x-x^2=(y^2-1)+2y-y^2} \\{x^2-1 \ge 0} \\{y^2-1 \ge 0} \\{x+y=a} \end{matrix} }\\{ \begin{Bmatrix} {-(x^2-1)+2x-x^2=(y^2-1)+2y-y^2} \\{x^2-1 < 0} \\{y^2-1 \ge 0} \\{x+y=a} \end{matrix} }\\{ \begin{Bmatrix} {(x^2-1)+2x-x^2=-(y^2-1)+2y-y^2} \\{x^2-1 \ge 0} \\{y^2-1 < 0} \\{x+y=a} \end{matrix} }\\{ \begin{Bmatrix} {-(x^2-1)+2x-x^2=-(y^2-1)+2y-y^2} \\{x^2-1 < 0} \\{y^2-1 < 0} \\{x+y=a} \end{matrix} } \end{matrix}\]](https://ege-resheniya.ru/wp-content/ql-cache/quicklatex.com-a7a364a371a8ce7a379a51c2b78e606f_l3.png)
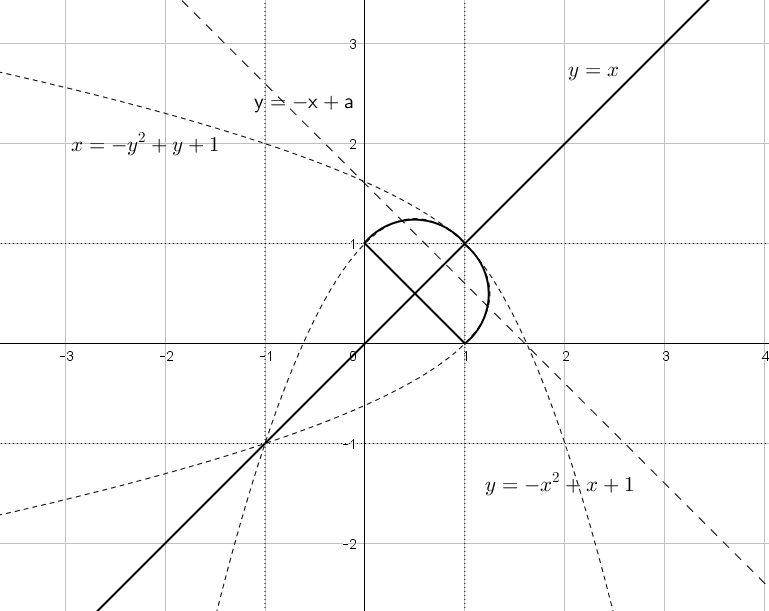
![Rendered by QuickLaTeX.com \[\begin{bmatrix} { \begin{Bmatrix} {y = x} \\{x^2-1 \ge 0} \\{y^2-1 \ge 0} \\{x+y=a} \end{matrix} }\\{ \begin{Bmatrix} {y=-x^{2} + x + 1 } \\{x^2-1 < 0} \\{y^2-1 \ge 0} \\{x+y=a} \end{matrix} }\\{ \begin{Bmatrix} {x = - y^{2} + y + 1} \\{x^2-1 \ge 0} \\{y^2-1 < 0} \\{x+y=a} \end{matrix} }\\{ \begin{Bmatrix} { -x^{2} + x = - y^{2} + y } \\{x^2-1 < 0} \\{y^2-1 < 0} \\{x+y=a} \end{matrix} } \end{matrix}\]](https://ege-resheniya.ru/wp-content/ql-cache/quicklatex.com-9f9dba4068fdaa1acf4cf58cb467a59a_l3.png)
![Rendered by QuickLaTeX.com \[\begin{bmatrix} { \begin{Bmatrix} {y = x} \\{x \in (-\infty; -1]\cup[1;+\infty)} \\{y \in (-\infty; -1]\cup[1;+\infty)} \\{y=-x+a} \end{matrix} }\\{ \begin{Bmatrix} {y=-x^{2} + x + 1 } \\{-1< x < 1} \\{y \in (-\infty; -1]\cup[1;+\infty)} \\{y=-x+a} \end{matrix} }\\{ \begin{Bmatrix} {x = - y^{2} + y + 1} \\{x \in (-\infty; -1]\cup[1;+\infty)} \\{-1< y < 1} \\{y=-x+a} \end{matrix} }\\{ \begin{Bmatrix} { (y-x)(y+x-1)=0} \\{-1< x < 1} \\{-1< y < 1} \\{y=-x+a} \end{matrix} } \end{matrix}\]](https://ege-resheniya.ru/wp-content/ql-cache/quicklatex.com-12d391a8b59b534a0c832ce22f51f70d_l3.png)
Ответ: ![]() .
.
Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров
Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru


