Решение задания 18, вариант 25, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике

Найти все значения a, при каждом из которых неравенство

$3x^5 +11x +4|x-a+3|+2|3x+a-5|+\sqrt[3]{4x+5} \le 25$

выполняется для всех значений $x \in [-4;-1]$ .

Заметим, что слева — возрастающая по $x$ функция, как бы ни раскрывались модули. Значит, максимум у нее в правом конце отрезка $x \in [-4;-1]$ . Значит, чтобы для всех $x$ из отрезка выполнялось неравенство, нужно, чтобы оно выполнялось на правом конце отрезка. Подставим $x=-1$ :

$-3-11+4|-a+2|+2|a-8|+1 \le 25$

$4|2-a|+2|a-8|\le 24+14=38$

$4|a-2|+2|a-8|\le 38$

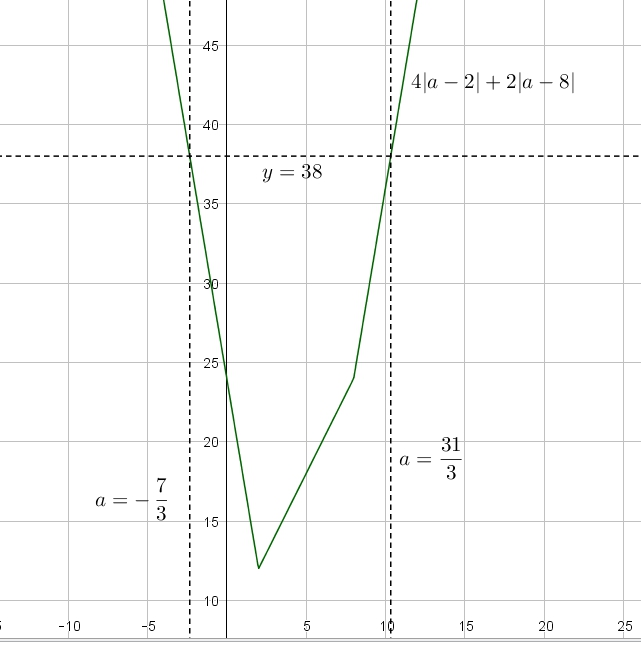
Рассмотрим три интервала, на которых раскроем модули: $(-\infty;2), (2;8), (8;+\infty)$ .
и заодно построим график функции $4|a-2|+2|a-8|$ :

$\begin{bmatrix} { \begin{Bmatrix} { 4(a-2)+2(a-8) \le 38 } \\{a \ge 8} \end{matrix} }\\{ \begin{Bmatrix} { 4(a-2)-2(a-8) \le 38 } \\{ 2 \le a < 8} \end{matrix} }\\{ \begin{Bmatrix} { -4(a-2)-2(a-8) \le 38 } \\{a < 2} \end{matrix} } \end{matrix}$

$\begin{bmatrix} { \begin{Bmatrix} { 6a- 24 \le 38 } \\{a \ge 8} \end{matrix} }\\{ \begin{Bmatrix} { 2a +8 \le 38 } \\{ 2 \le a < 8} \end{matrix} }\\{ \begin{Bmatrix} { -6a +24 \le 38 } \\{a < 2} \end{matrix} } \end{matrix}$

$\begin{bmatrix} { \begin{Bmatrix} { 6a \le 62} \\{a \ge 8} \end{matrix} }\\{ \begin{Bmatrix} { 2a \le 30} \\{ 2 \le a < 8} \end{matrix} }\\{ \begin{Bmatrix} { -6a \le 14} \\{a < 2} \end{matrix} } \end{matrix}$

$\begin{bmatrix} { \begin{Bmatrix} { a \le \frac{31}{3}} \\{a \ge 8} \end{matrix} }\\{ \begin{Bmatrix} { a \le 15} \\{ 2 \le a < 8} \end{matrix} }\\{ \begin{Bmatrix} { a \ge -\frac{7}{3}} \\{a < 2} \end{matrix} } \end{matrix}$

$\begin{bmatrix} { \begin{Bmatrix} { a \in [8; \frac{31}{3}] } \end{matrix} }\\{ \begin{Bmatrix} { 2 \le a < 8} \end{matrix} }\\{ \begin{Bmatrix} { a \in [-\frac{7}{3};2)} \end{matrix} } \end{matrix}$

Ответ: $a \in [-\frac{7}{3};\frac{31}{3}]$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru