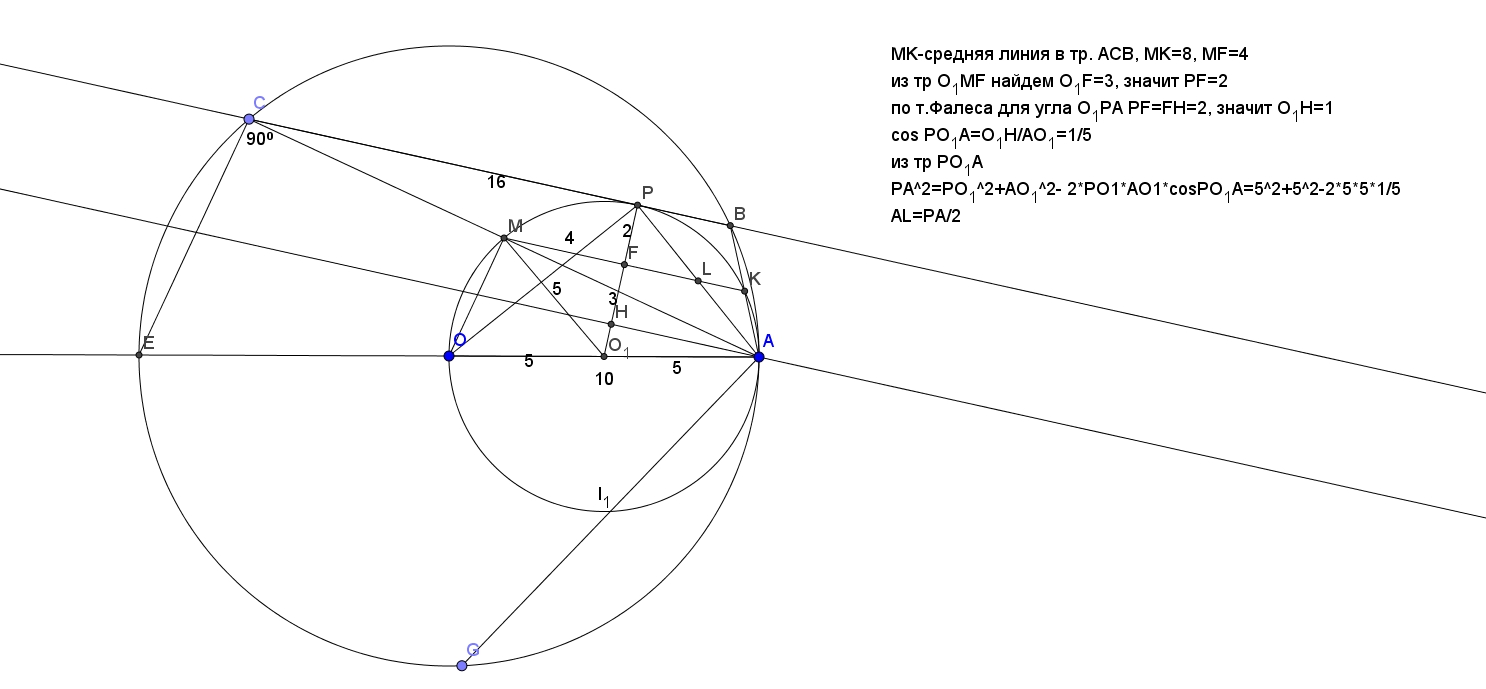
Решение задания 16, вариант 11, Ященко 36 вариантов, ЕГЭ-2017 — Решения вариантов ЕГЭ по математике

M — середина отрезка AC , K — середина отрезка AB , — из подобия треугольников AEC и AOM (по двум углам — один общий, другой — 90 градусов, т.к диаметры ).

Значит MK — средняя линия, параллельна CB и равна 8.

Чтобы найти AL, надо найти AP = 2* AL (т.к. MK — средняя линия)

AP найдем из прямоугольного треугольника OPA по теореме Пифагора

Найдем OP по теореме косинусов из треугольника $OO_1P$

из прямоугольного тр $O_1MF$ по теореме Пифагора найдем $O_1F=3$ , значит PF=2
по т.Фалеса для угла $O_1PA$ $PF=FH=2$ , значит $O_1H=5-2-2=1$

Косинус угла $PO_1A$ = 1/5, т.к. $MK=8$ и OP бьется в соотношении 1:2:2 параллельными линиями (PF:FH=2:2 по т. Фалеса, а 1 — смотри выше вычисление $O_1H$ ).

$OP^2= 5^2+5^2-2*5*5*cosOO_1P= 25+25+2*5*5*1/5 = 60$

$PA^2=10^2-60=40;$
$PA=\sqrt{40}=2*\sqrt{10}; AL=\sqrt{10}$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru