Решение задания 16, вариант 10, Ященко 36 вариантов, ЕГЭ-2017

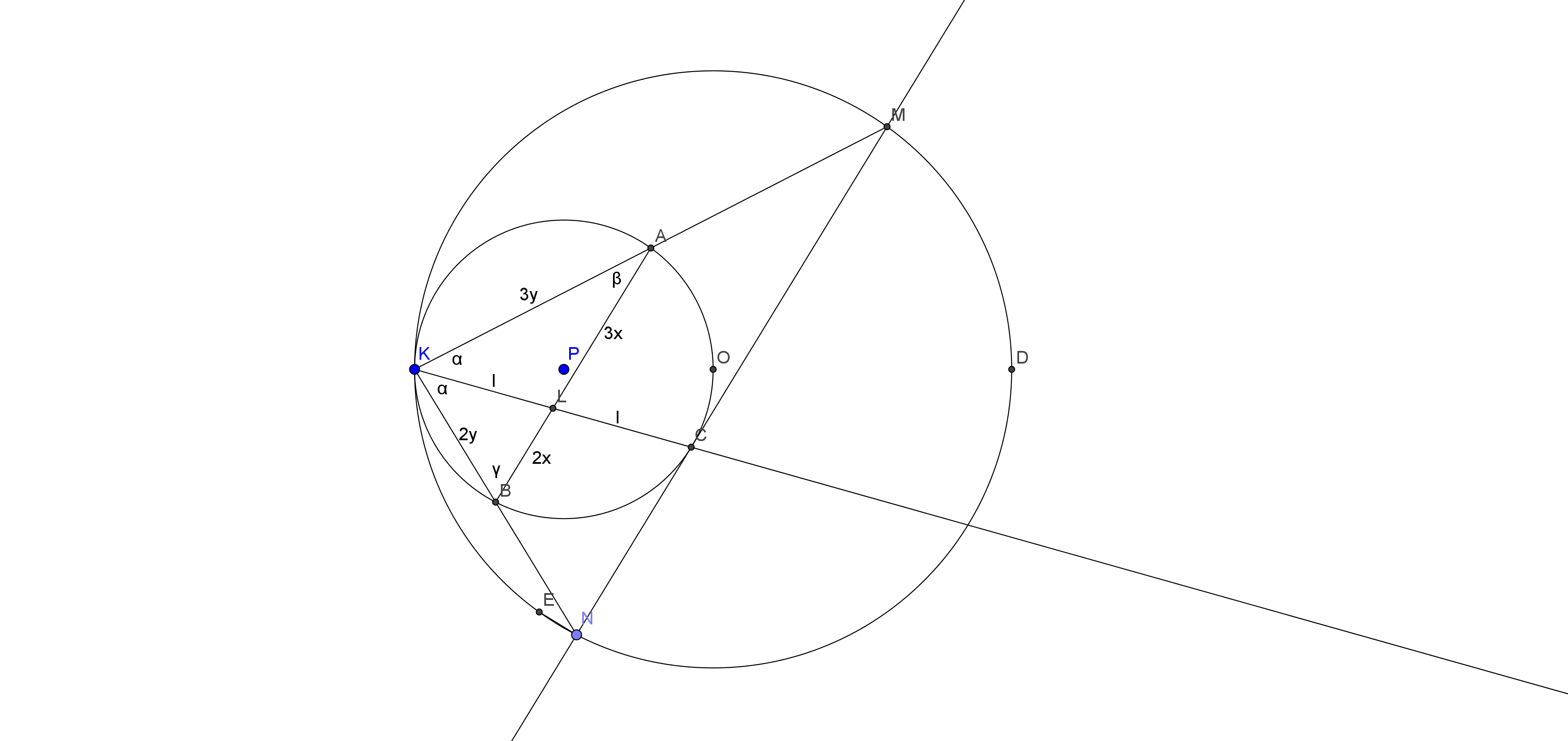
Основные идеи:
Точки A и B — середины KM и KN соответственно, т.к. внутренняя окружность проходит через центр внешней и т.к. по двум углам ().
как средняя линия.
Т.к. , то дуги BC и AC равны (т.к. , то , а опирается на дугу и поэтому равен ),
т.е. и дуги BC и AC равны.
Т.к. дуги равны, то KC — биссектриса угла BKA, обозначим его за , а — за — за.
Т.к. KC — биссектриса, то
Т.к. AB — средняя линия, то с коэффициентом 1/2.
Поэтому
и по свойству биссектрисы
Обозначим
Найдем соотношения между , которые приведут нас в итоге к нахождению и ответу в задаче.
Заметим, что — по свойству хорд.
Также вспомним формулу длины биссектрисы — . Обозначим .
Итак, (хорды) и (длина биссектрисы).
Получаем .
Теперь запишем теоремы синусов и косинусов.


.

Т.к. , где — радиус меньшей окружности, то
,
откуда, сокращая на ,
,
и подставляя найденные выше связи между углами, получаем
,
),
),
),
— фундаментальный результат, мы нашли угол !
Дальше легко:


Найдем sin из cos: