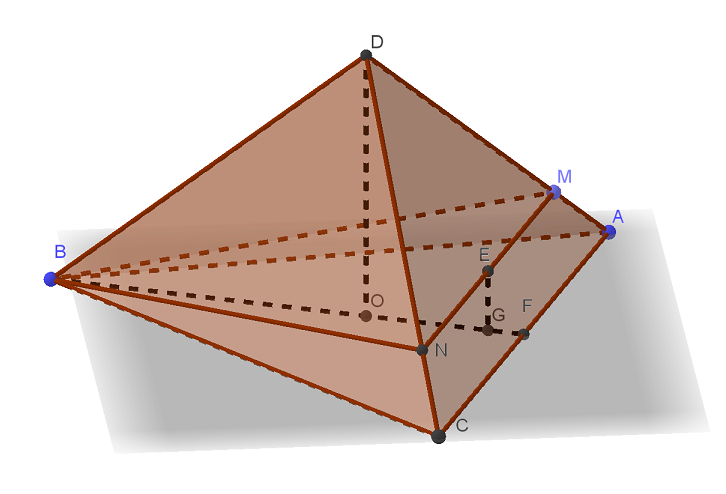
Решение задания 14, вариант 4, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике

В пирамиде ABCD рёбра DA, DB и DC попарно перпендикулярны, а AB = BC = AC = 14.
а) Докажите, что эта пирамида правильная.
б) На рёбрах DA и DC отмечены точки M и N соответственно, причём DM:MA = DN:NC = 6:1. Найдите площадь сечения MNB.
Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке https://ggbm.at/UB5t3Mue

Треугольники ABD, BCD, ACD имеют углы D=90 градусов, т.е. это прямоугольные треугольники.
Обозначим за x,y,z стороны ребра DA, DB, DC, напишем теорему Пифагора:

$x^2+y^2=196$

$x^2+z^2=196$

$y^2+z^2=196$

Вычитая из 2го 1е, получим $y=z$ , из 3го — 2е, что $x=y$ , т.е.

$x=y=z=\frac{14}{\sqrt{2}}=DA=DB=DC=7\sqrt{2}$

, длины наклонных одинаковы, значит длины проекций тоже одинаковы и проекция точки D попадает в центр правильного тр. ABC, и пирамида — правильная.

$MN=\frac67AC=12$

$BG=\frac{20}{21}BF$

$EG=\frac17DO$

$BE^2=(\frac{20}{21}BF)^2+(\frac17DO)^2$

$BF=14*\frac{\sqrt3}{2}=7\sqrt{3}$

$DO^2=(7\sqrt{2})^2-(\frac23BF)^2=49*2-\frac{4*49}{3}$

$DO=7\sqrt{\frac23}$

$BE^2=\frac{400}{3}+\frac23=\frac{402}{3}=134$

$BE=\sqrt{134}$

$S=\frac12BE*NM=\frac12*\sqrt{134}*12=6\sqrt{134}$

Второе решение:

$BE^2=BN^2-NE^2=BD^2+DN^2-NE^2=(7\sqrt{2})^2+(6\sqrt{2})^2-6^2=134$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru