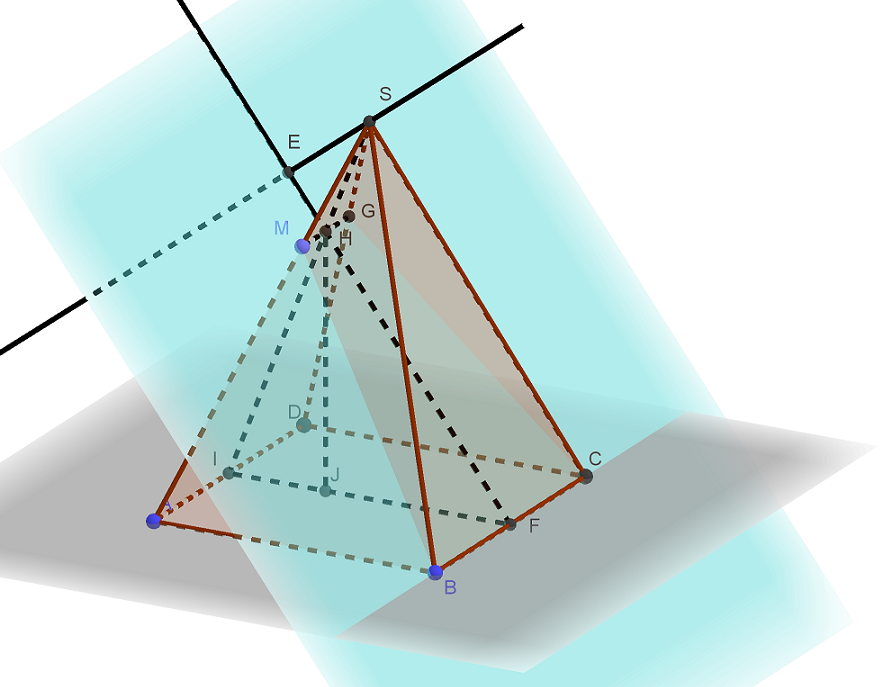
Решение задания 14, вариант 18, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике

В правильной четырёхугольной пирамиде SABCD основание ABCD — квадрат со стороной 6, а боковое ребро равно 9. На ребре SA отмечена точка М так, что AM = 6.
а) Постройте перпендикуляр из точки S на плоскость ВСМ.

б) Найдите расстояние от вершины S до плоскости ВСМ.
Трехмерная картинка, которую можно крутить в 3D, доступна по ссылке
https://ggbm.at/DmEJfxZZ

$SI=\sqrt{9^2-3^2}=\sqrt{72}$

$IH=\frac23\sqrt{72}$

$HJ=\frac23*\sqrt{72-3^2}=\frac23\sqrt{63}$

$\cos \angle HIJ=\frac{IJ}{HI}=\frac{3*2}{2\sqrt{72}}=\frac{3}{\sqrt{72}}$

По теореме косинусов

$HF^2=\frac49*72+36-2*\frac23\sqrt{72}*6*\frac{3}{\sqrt{72}}=44$

Найдем $\cos \angle IHF$ опять по теореме косинусов:

$6^2=(\frac23\sqrt{72})^2+(\sqrt{44})^2-2*\frac23\sqrt{72}*\sqrt{44}*\cos\angle IHF$

$36=\frac49*72+44-\frac43 \sqrt{72}*\sqrt{44}*\cos\angle IHF$

$-40=-4 \sqrt{8}*\sqrt{44}*\cos\angle IHF$

$\cos \angle IHF =\frac{10}{\sqrt{8}*\sqrt{44}}=\frac{5}{\sqrt{8}*\sqrt{11}}$

$\sin \angle SHE=\sqrt{1-\frac{25}{88}}=\sqrt{\frac{63}{88}}$

$ES=SH*\sin\angle SHE=\frac13\sqrt{72} \sqrt{\frac{63}{88}}=\sqrt{\frac{9*7}{11}}=3\sqrt{\frac{7}{11}}$

Второе решение.
Напишем теорему синусов:

$\frac{HF}{\sin\angle HIF}=\frac{IF}{\sin\angle IHF}$

$\frac{\sqrt{44}}{\sqrt{\frac{63}{72}}}=\frac{6}{\sin\angle IHF}$

$\sin\angle IHF=\frac{6*\sqrt{63}}{\sqrt{44}\sqrt{72}}$

$SE=SH*\sin\angle SHE=\frac13\sqrt{72}*\frac{6*\sqrt{63}}{\sqrt{44}\sqrt{72}}=3\sqrt{\frac{7}{11}}$

Третье решение.
Введем систему координат с центром в точке F, ось x — в сторону т.С, ось Y — в сторону т.J, ось z — вверх.
Тогда координаты точек: $C(3;0;0); F(0;0;0); H(0;4;\sqrt{28}); S(0;3;\sqrt{63})$
Напишем уравнение плоскости (CFH): $Ax+By+Cz+D=0$
Найдем числа $A,B,C,D$ , подставим точки C,F,H в уравнение плоскости (CFH):
C(3;0;0): $A*3+B*0+C*0+D=0 => 3A=-D$
F(0;0;0): $A*0+B*0+C*0+D=0 => D=0, A=0$
$H(0;4;\sqrt{28})$ : $A*0+B*4+C*\sqrt{28}+D=0 => B*4+C*\sqrt{28}=0;$
Можно взять $B=-\sqrt{28}; C=4$
Итак, уравнение плоскости (CFH): $0x-\sqrt{28}y+4z+0=0$
Расстояние между точкой $(x,y,z)$ и плоскостью $Ax+By+Cz+D=0$ имеет вид:

$\frac{Ax+By+Cz+D}{\sqrt{A^2+B^2+C^2}}$

Найдем расстояние от т. $S(0;3;\sqrt{63})$ до плоскости $0x-\sqrt{28}y+4z+0=0$ :

$h=\frac{0*0-\sqrt{28}*3+4\sqrt{63}+0}{\sqrt{0^2+28+4^2}}=\frac{-2*3\sqrt{7}+4*3\sqrt{7}}{\sqrt{44}}= \frac{2*3\sqrt{7}}{\sqrt{44}}=3\sqrt{\frac{7}{11}}$

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru