Решение задания 18, вариант 4, Ященко 36 вариантов, ЕГЭ-2018 — Решения вариантов ЕГЭ по математике

Найти все значения a, при каждом из которых уравнение

$(8x-5) \cdot \ln(x+a) = (8x-5) \cdot \ln(3x-a)\]$

имеет ровно один корень на отрезке $[0;1]$ .

Напишем ОДЗ:

$\begin{Bmatrix}{x+a > 0}\\{3x-a >0 }\end{matrix}$

$\begin{Bmatrix}{a>-x}\\{a<3x }\end{matrix}$

Вынесем $(8x-5)$ за скобку:

$(8x-5) \cdot \{ \ln(x+a) - \ln(3x-a) \}=0$

Получаем первый корень $x_1=\frac58$ , подставляем его в ОДЗ и получаем ограничения на $a$ :

$\begin{Bmatrix} {x_1=\frac58}\\ {a>-x_1=-\frac58}\\{a<3x_1=\frac{15}{8} }\end{matrix}$

Т.е. мы получили корень $x_1=\frac58$ при $-\frac58<a<\frac{15}{8}$ . При этом этот корень нам подходит — он лежит на отрезке $[0;1]$ . Ищем второй корень:

$x+a=3x-a$

$x=a$

Подставим второй корень $x_2=a$ в ОДЗ, чтобы найти ограничения на $a$ :

$\begin{Bmatrix}{a>-x_2}\\{a<3x_2 }\end{matrix}$

$\begin{Bmatrix}{a>-a}\\{a<3a }\end{matrix}$

$2a>0$

$a>0$

Итак, второй корень $x_2=a$ существует при $a>0$ , соответственно, если мы рассматриваем отрезок $[0,1]$ , то второй корень $x_2$ существует не на всем этом отрезке, а только на его подмножестве $(0,1]$ .

Нам нужно, чтобы на отрезке $x \in [0,1]$ корень был единственным.

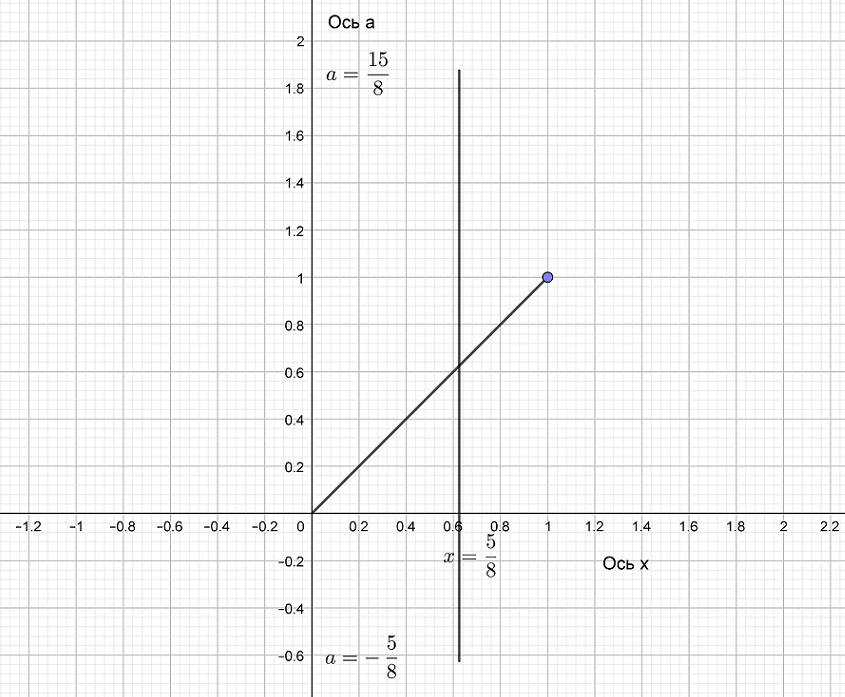
Нарисуем на плоскости (a,x) наши корни:

Ответ: Только один корень будет при

$a \in (-\frac58,0]\cup \{\frac58\} \cup (1,\frac{15}{8})$

Это будет первый корень $x_1=\frac58$ .
При остальных $a$ , т.е. при $a \in (0,\frac58) \cup (\frac58,1]$ — будут два корня — и $x_1=\frac58$ , и $x_2=a$ .

Вы тонете в океане математики и физики? Давайте спасаться вместе!
Получи запись бесплатного вебинара
с разбором задач, которые были на реальном ЕГЭ-2019 (29 мая 2019г.),
получи условия и ссылки на решения некоторых задач
с реальных ЕГЭ-2017 (2 июня 2017) и ЕГЭ-2018 (26 июня 2018),
получи видеоразбор решений 11й,12й,13й,14й,15й, 16й,17й,18й задач
из варианта 7 книжки "Ященко 36 вариантов 2019",
видеозаписи прошлых вебинаров

Получить ссылки на вебинар и на видео. Нажимай!
C уважением, репетитор Павел Коваленко,
создатель сайта ege-resheniya.ru

2 комментария к “Решение задания 18, вариант 4, Ященко 36 вариантов, ЕГЭ-2018”

Скажите пожалуйста, почему там один корень, когда промежуток принадлежит от [-5/8;0]. Если включить ноль, то получится два корня (сам ноль и 5/8 на оси ОХ)

репетитор Павел Коваленко:

06.05.2018 в 13:07

В точке a=0 у нас только один корень x=5/8, и нет второго корня x=a(и равного нулю), т.к. подставив x=a=0 в исходный уравнение, вы не сможете извлечь логарифм от нуля, т.е. не пройдете проверку по ОДЗ.

Комментарии закрыты.